Eliminación de Gauss - Jordan
Introducción
Los métodos de eliminación de Gauss y de Gauss-Jordan nos permiten obtener las soluciones (en caso de haberlas) de los sistemas de ecuaciones lineales (SEL). Ambos métodos se basan en la idea de que las soluciones del SEL que se obtiene al realizar operaciones elementales fila o columna son las mismas que las del SEL original.
Notación
Consideremos un SEL con incógnitas cuya forma matricial es , donde es la matriz formada por los coeficientes de las ecuaciones, es el vector columna formado por todas las incógnitas del SEL () y es la columna de los términos independientes de las ecuaciones.
Trabajaremos con la matriz ampliada del SEL, que es la matriz que tiene la matriz a la izquierda y el vector a la derecha, separados por una línea: .
Ejemplo
El sistema
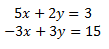
tiene la matriz ampliada
El método de Gauss-Jordan
- En cada fila, el primer elemento distinto de cero (de izquierda a derecha) es un 1 (uno principal). A la izquierda de este 1, sólo hay ceros. A su derecha puede haber cualquier número. En la columna del 1 principal de las filas de arriba y las de abajo sólo puede haber ceros (a no ser que sea la primera fila y por encima del 1 no hay ningún elemento).
- El uno principal de cualquier fila se sitúa más a la izquierda de los unos principales de las filas inferiores a ésta.
- Si existen filas formadas únicamente por ceros, éstas son las inferiores.
Multiplicamos la primera fila por 1/5 y la segunda por 1/3
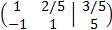
Sumamos a la segunda fila la primera
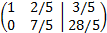
Multiplicamos la segunda fila por 5/7
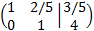
Sumamos a la primera fila la segunda fila multiplicada por -2/5
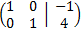
Ahora escribimos el sistema que representa esta última matriz:
Es decir, hemos obtenido la solución del sistema.