Uitleg + opgaven 27, 28 en 29
Hellingsgrafiek
Bekijk de applet. Schuif punt P op de grafiek.
Bekijk de grafiek van de functie f(x) = x2 met daarin de raaklijn aan de grafiek in het punt(1,1). De richtingscoëfficiënt van die raaklijn bepaalt de helling van de grafiek bij x = 1.
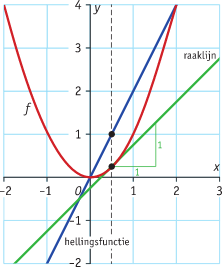
Als je de waarden van x verandert, veranderen ook de hellingsgetallen van de raaklijnen. Je kunt van die hellingsgetallen een afzonderlijke grafiek maken: de hellingsgrafiek. De bijbehorende functie wordt de hellingsfunctie f'(x) genoemd. Beweeg punt P over de grafiek en ga na dat de hellingsgetallen van de raaklijn overeen komen met de functiewaarden van de hellingsgrafiek.
Als je de grafiek van de functie f en die van zijn hellingsfunctie f' vergelijkt, dan valt op:
- als de grafiek stijgend is, zijn de hellingsgetallen positief (en omgekeerd);
- als de grafiek dalend is, zijn de hellingsgetallen negatief (en omgekeerd);
- in toppen van de grafiek (en dus extremen van de functie) is het hellingsgetal 0 .
Opgave 27
Bekijk de grafiek van f(x) = x2 in de uitleg.
Bepaal voor elke waarde van x uit de tabel het bijbehorende differentiaalquotiënt. Teken vervolgens met die gegevens de hellingsgrafiek van f.
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| f'(x) |
Opgave 28
Gegeven is de functie f(x) = -x2. Bepaal voor elke waarde van x uit de tabel het bijbehorende differentiaalquotiënt. Teken vervolgens met die gegevens de hellingsgrafiek van f.
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| f'(x) |
Opgave 29
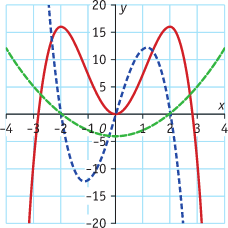
Bekijk de grafiek (rood) en twee hellingsgrafieken (groen en blauw gestippeld). Welke hellingsgrafiek hoort bij de rode grafiek?