Ángulo al centro y ángulo inscripto
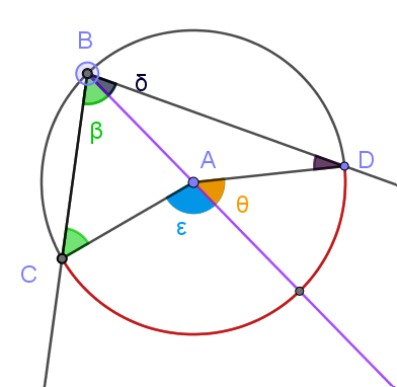
En esta actividad analizaremos la relación entre las amplitudes de un ángulo inscripto y su correspondiente ángulo al centro (entendiendo por ángulo correspondiente el que abarca el mismo arco):
Mueve el deslizador y analiza las amplitudes del ángulo inscripto y el ángulo al centro. Plantea tus conclusiones
¿Cuál es el ángulo inscripto?
¿Cuál es el ángulo al centro?
¿Cuál es la amplitud del ángulo al centro cuando el ángulo inscripto tiene 59° de amplitud?
¿Cuál es la amplitud del ángulo al centro cuando el ángulo inscripto tiene 23°?
¿Cuál es la amplitud del ángulo inscripto cuándo el ángulo al centro tiene 162° de amplitud?
Analiza si encuentras alguna relación entre las amplitudes de los ángulos al centro e inscripto, escribe las conclusiones de tú análisis.
Analiza la relación entre las amplitudes del ángulo inscripto y su correspondiente ángulo al centro a partir de sumar los ángulos interiores del triángulo ABC
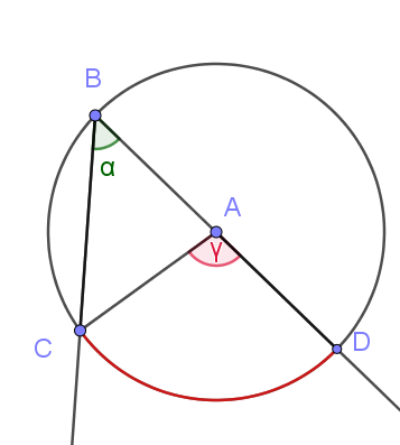
Plantea la suma de las amplitudes de los ángulos del triángulo BAC a partir de alfa y gamma. ¿Cuál es la relación que obtienes?
CBD es un ángulo inscripto y CAD es el ángulo al centro correspondiente.