Degrees-Radians, area of sector and length of arcs
Keywords
| Degrees-Radians conversion | 度-ラジアン変換 | 도-라디안 변환 | 度与弧度转换 |
| Arc length | 弧の長さ | 호 길이 | 弧长 |
| Sector area | 扇形の面積 | 부채꼴 면적 | 扇形面积 |
| Area of a sector formula | 扇形の面積の公式 | 부채꼴의 면적 공식 | 扇形面积公式 |
Inquiry questions
| Factual Questions: What is the formula for converting degrees to radians, and how is it applied in calculations? How do you calculate the length of an arc given its central angle in radians? What steps are involved in finding the area of a sector using its central angle in radians? | Conceptual Questions: How do degrees and radians represent different ways of measuring angles, and what are the advantages of each? In what ways do the concepts of arc length and sector area extend our understanding of circles and their geometric properties? How does the concept of radians link to the real-world phenomena, such as the movement of a pendulum or the design of a pizza slice? | Debatable Questions: Why might mathematicians and scientists prefer radians over degrees in professional contexts, and can there be situations where degrees are more useful? Considering the practical applications of arc lengths and sector areas in fields like engineering and architecture, how essential is it for professionals in these fields to have a strong grasp of these concepts? Is the shift towards a more radian-centric approach in education justified by the needs of modern scientific and engineering practices, or does it overlook the intuitive understanding provided by degrees? |
Part 1 - Opening problem
Opening problem diagram

Opening problem
Peter and William, two friends with a shared pizza passion, faced a challenge. Preferring different parts of a large, sector-shaped slice, they wondered how to split it equally from point A to point B. Could an app, designed for such puzzles, reveal the exact angle at the slice's tip? Their quest for the answer turned a simple meal into an intriguing mathematical adventure. Can you find the approximate angle required? Is it affected by the radius of the pizza?
Opening problem - Applet to explore
The Radian Quest

1. Circle of Radians: - In your own words, explain how to convert between degrees and radians, and back.
2. Click on the Arcs and sectors button. Arc Length Adventure: - Using the arc length formula, calculate the length of an arc for a given angle in radians. - Pose a real-world problem: "If a pendulum swings through an angle of π/6 radians, what is the length of the arc traced by the pendulum's path?"
3. Arc and Sector Scenarios: - How can knowing the arc length and sector area be useful in fields such as engineering or architecture?
3. Sector Area Saga: - Apply the area of a sector formula to find the area for a given angle in radians. - Challenge: "A sector of a circle has a central angle of π/4 radians, what fraction of the circle's area does this sector represent?"
Questions for Investigation: 1. Conversion Challenge: - Given a random angle in degrees, can you convert it to radians without a calculator?
2. Radian Realities: - Why do mathematicians and scientists prefer to use radians over degrees in many calculations?
Part 2 - Additional resource
Part 3 - Practising with Exam style questions on areas of sectors and arc lengths
Useful additional formula for some of the exam-style questions
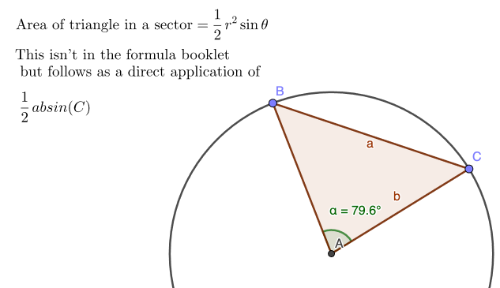
[MAA 3.4] ARCS AND SECTORS
[MAA 3.4] ARCS AND SECTORS_solutions
Engagement Activities: - "Radian Art": Create a design using different arc lengths and sector areas. - "Radian Race": A game where participants must quickly convert degrees to radians and vice versa. Throughout the investigation, the Radian Quest will unveil the circular constants of the universe, making the journey an angle of epic proportions.
![[MAA 3.4] ARCS AND SECTORS.pdf](https://stage.geogebra.org/resource/jvprqqdp/DwwCgdztv3L9N2iV/material-jvprqqdp-thumb.png)
![[MAA 3.4] ARCS AND SECTORS_solutions.pdf](https://stage.geogebra.org/resource/cxmuhpey/v6PJu2J9h1ioM7vt/material-cxmuhpey-thumb.png)

