Geometría analítica
INTRODUCCIÓN A LA GEOMETRÍA ANALÍTICA
GEOMETRÍA ANALÍTICA
1.1 Sistemas de Coordenadas Rectangulares
Las coordenadas cartesianas o coordenadas rectangulares (plano cartesiano) son un tipo de coordenadas
ortogonales usadas en espacios euclídeos, para la representación gráfica de una función, en geometría analítica, o del movimiento o posición en física, caracterizadas porque usa como referencia ejes ortogonales entre sí que se cortan en un punto origen. Las coordenadas cartesianas se definen así como la distancia al origen de las proyecciones ortogonales de un punto dado sobre cada uno de los ejes. La denominación de ‘cartesiano’ se introdujo en honor de René Descartes, quien lo utilizó de manera formal por primera vez.
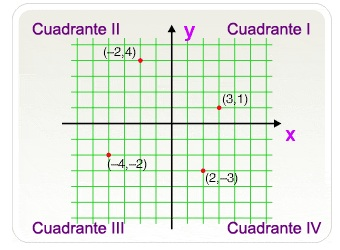
Si el sistema en sí es un sistema bidimensional, se denomina plano cartesiano. El punto de corte de las rectas se hace coincidir con el punto cero de las rectas y se conoce como origen del sistema. Al eje horizontal o de las abscisas se le asigna los números enteros de las equis (“x”); y al eje vertical o de las ordenadas se le asignan los números enteros de las yes (“y”). Al cortarse las dos rectas, dividen al plano en cuatro regiones o zonas, que se conocen con el nombre de cuadrantes:
Las coordenadas cartesianas se usaron un ejemplo para definir un sistema cartesiano o sistema de referencia respecto ya sea a un solo eje (línea recta), respecto a dos ejes (un plano) o respecta tres ejes (en el espacio), perpendiculares entre sí (plano y espacio), que se cortan en un punto llamado origen de coordenadas. En el plano, las coordenadas cartesianas se denominan abscisa y ordenada. La abscisa es la coordenada horizontal y se representa habitualmente por la letra x, mientras que la ordenada es la coordenada vertical y se representa por la y.
Si tenemos un sistema de referencia formado por tres rectas perpendiculares entre sí (X, Y, Z) (terna ordenada), que se cortan en el origen (0, 0, 0), cada punto del espacio puede nombrarse mediante tres números: (x, y, z), denominados coordenadas del punto, que son las distancias ortogonales a los tres planos principales: los que contienen las parejas de ejes YZ, XZ e YX, respectivamente.
1.2 Distancia entre Dos Puntos
Por haberlo estudiado, sabemos que el Plano Cartesiano se usa como un sistema de referencia para localizar puntos en un plano. Otra de las utilidades de dominar los conceptos sobre el Plano cartesiano radica en que, a partir de la ubicación de las coordenadas de dos puntos es posible calcular la distancia entre ellos. Cuando los puntos se encuentran ubicados sobre el eje x (de las abscisas) o en una recta paralela a este eje, la distancia entre los puntos corresponde al valor absoluto de la diferencia de sus abscisas (x2 – x1) .
Ejemplo:
Calcula la distancia entre los puntos P1(7,5) y P2(4, 1)
- Primer cuadrante “I”: Región superior derecha
- Segundo cuadrante “II”: Región superior izquierda
- Tercer cuadrante “III”: Región inferior izquierda
- Cuarto cuadrante “IV”: Región inferior derecha
Las coordenadas cartesianas se usaron un ejemplo para definir un sistema cartesiano o sistema de referencia respecto ya sea a un solo eje (línea recta), respecto a dos ejes (un plano) o respecta tres ejes (en el espacio), perpendiculares entre sí (plano y espacio), que se cortan en un punto llamado origen de coordenadas. En el plano, las coordenadas cartesianas se denominan abscisa y ordenada. La abscisa es la coordenada horizontal y se representa habitualmente por la letra x, mientras que la ordenada es la coordenada vertical y se representa por la y.
Si tenemos un sistema de referencia formado por tres rectas perpendiculares entre sí (X, Y, Z) (terna ordenada), que se cortan en el origen (0, 0, 0), cada punto del espacio puede nombrarse mediante tres números: (x, y, z), denominados coordenadas del punto, que son las distancias ortogonales a los tres planos principales: los que contienen las parejas de ejes YZ, XZ e YX, respectivamente.
1.2 Distancia entre Dos Puntos
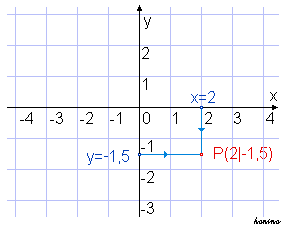
Por haberlo estudiado, sabemos que el Plano Cartesiano se usa como un sistema de referencia para localizar puntos en un plano. Otra de las utilidades de dominar los conceptos sobre el Plano cartesiano radica en que, a partir de la ubicación de las coordenadas de dos puntos es posible calcular la distancia entre ellos. Cuando los puntos se encuentran ubicados sobre el eje x (de las abscisas) o en una recta paralela a este eje, la distancia entre los puntos corresponde al valor absoluto de la diferencia de sus abscisas (x2 – x1) .
Ejemplo:
Calcula la distancia entre los puntos P1(7,5) y P2(4, 1)
Para mayor apoyo del texto ver el video de forma atenta
4 cuadrantes en un plano cartesiano
GEOMETRÍA ANALITICA
gráfica de puntos en geogegra en un plano cartesiano
distancia entre dos puntos
EVALUACIÓN DE GEOMETRÍA ANALÍTICA
¿CUANTOS CUADRANTES TIENE UN SISTEMA DE COORDENADAS?
2. GRAFICAR LOS PUNTOS A(1,3); B(-3,5) EN GEOGEBRA Y COLOCAR EL ENLACE EN ESTE APARTADO
3. CALCULAR LA DISTANCIA DE A(7,8); B(-5,-8)EN GEOGEBRA Y COLOCAR EL ENLACE EN ESTE APARTADO