Projective Geometry: Homography, Cross-ratio, Harmonic Conjugates, Polarity
Projective geometry is the geometry of what we see in real life where paralel lines meet at the horizon and circles are seen as ellipses. Those effects are the result of cone-shaped projection: light rays from objects come to the eye, or in reverse, light rays from a flashlight shine objects and cast shadow on a screen.
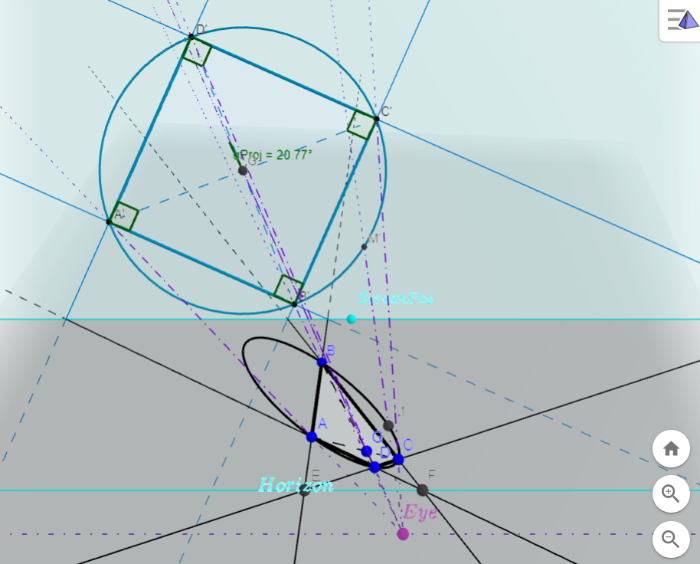
Here we use circled squares as objects of projection between a "ground" plane and a slanted "screen": (see this 3D applet)
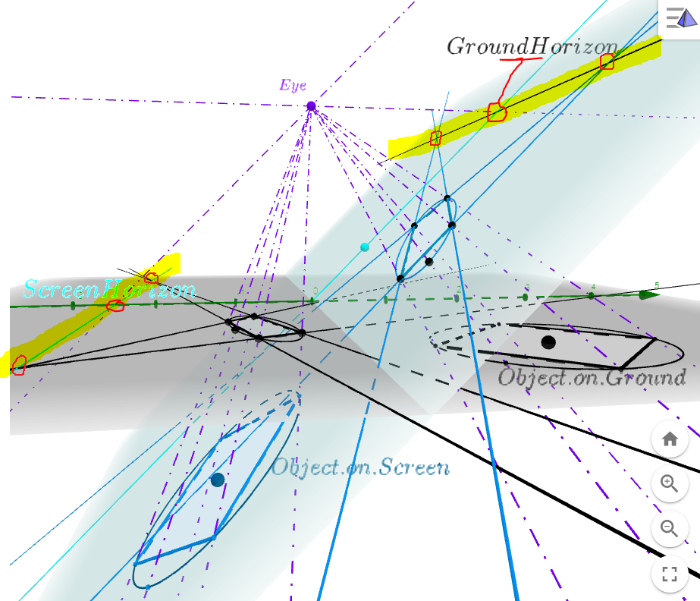
We can see the object on the ground is projected into an image on the screen as well as the object on the screen is projected into an image on the ground. Thus each plane can be both object plane and image plane. As image planes, the screen contains a vanishing line of the ground (ground horizon) and the ground contains a vanishing line of the screen (screen horizon), which are yellow high lighted.
Let's turn aside to see clearer, reducing from 3D to 2D:
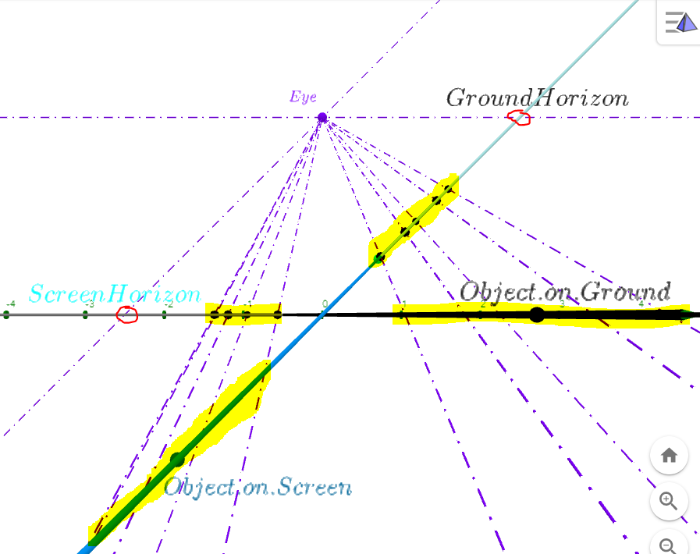
Perspectivity & Projectivity
Here on 2D space, we have object/image lines containing points (yellow high lighted) instead of object/image planes, and vanishing points (red marked) instead of vanishing lines. The object points and the corresponding image points are in perspective, and the mapping between them is called perspectivity, the simplest projective transformation. In reverse, for any two lines h and ℓ (see applet below), a triple of points (N, P, E) on h is in perspective with a triple of points (N', P', E') on ℓ only if the three projection lines NN', PP', EE' are concurrent, i.e. they meet at a single point V. In other words, any two couples of points (N, P) and (N', P') determine a perspectivity from V = NN' ∩ PP', which maps any other point, like E ∈ h to E' = VE ∩ ℓ and I ∈ h to I' = VI ∩ ℓ.
But how about two arbitrary triples of colinear points?
Two arbitrary triples of colinear points determine a projectivity or homography which is the general form of projective transformation including both single perspectivity and composition of perspectivities. The projectivity is not very much different from the perspectivity in that any projectivity can be decomposed into at most two perspectivities, and a self projectivity (identical mapping) can be decomposed into three distint perspectivities. That's the content of the fundamental theorem of projective geometry:
Cross-ratio
Projective transformation does not preserve distance nor ratio between distances, but it preserves the cross-ratio (the ratio of ratio) between four colinear points. So, cross-ratio is the crucial measure defining the structure of projective spaces.
The cross-ratio of quadruple of colinear points (N, P, E, I) is defined using signed segments (i.e. NP = -PN):
Here, when we perspectively project (N, P, E, I) from object line h onto image line , we have the perspective image (N', P', E', I') with the same cross-ratio (N', P'; E', I') = (N, P; E, I), for any center of perspectivity V (view point, eye or light source) and any image line . That means if two images (N, P, E, I) and (N', P', E', I') are in perspective, then their cross-ratios are the same.
For general projectivity (homography), we use Pappus's hexagon theorem to construct the intermediate image line g to decompose the projectivity into two perspectivities .
Here, we have the equivalence between projectivity and cross-ratio equality:
Harmonic conjugates
When the cross-ratio (N, P; E, I) = −1, they are called harmonic conjugates (harmonic points) where E and I harmonically conjugate with each other with respect to N and P. And because (E, I; N, P) = (N, P; E, I), N and P also harmonically conjugate with each other with respect to E and I. Because cross-ratio is invariant under projectivity, for any view point V not lying on h, we have four harmonic rays or harmonic straights (VN, VP, VE, VI) which project onto any line a quadruple of harmonic points like (N', P', E', I').
Three Metrics: Perspective, Exponential, Growth [...editing...]
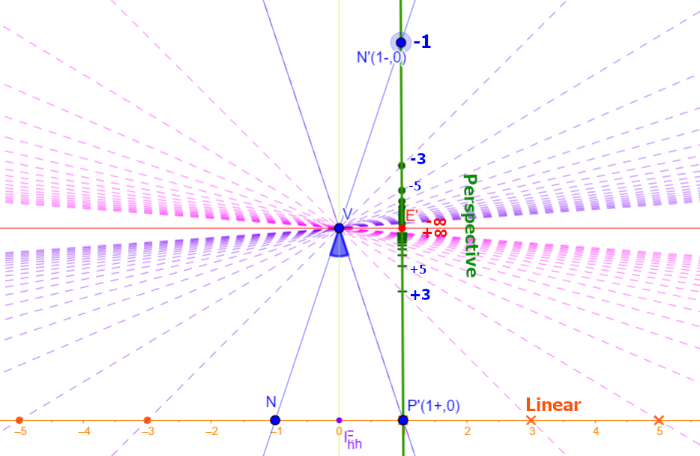
The quadruple of harmonic points (N, P, E, I) determines the basis of the perspective metric: N, P are unit points (-1, +1) and E, I are central points (0, ∞). This metric is reciprocally linear, i.e. the reciprocal of distance to the vanishing point E increases linearly:
, (Pk, P; E, ∞) = c/k, (?) where N = P-1, I = P0 and P = P1.
Because (N, P; E, I) = -1, the actual basis reduces to only 3 free points (P, E, I), where the 4th point N can be calculated from those 3 points. The basis triple (P, E, I) of perspective metric corresponds to (1, ∞, 0) in linear metric, where any point P-x has cross-ratio (P-x, P; E, I) = (-x, 1; ∞, 0) = -x exactly ...?... x = (x, 1; 0, ∞) for arbitrary x ranging from -∞ to +∞.
Note that in this page, only odd points P2k-1 are shown, because N is used in the place of I, i.e. (P2k-1, P; E, N) = k, and I is ignored in the perspective metric and exponential metric (I will takes different role in growth metric).
That reciprocal linearity is how we see the array of light poles on the street. And that also means when we project it onto a screen ℓ parallel to the ray VE from view point V to vanishing point E (click "Make Para∥el", chose "ℓ ∥ VE" in the applet above), the metric becomes linear as normal.

To see the whole image of perspective metric, we wrap the line ℓ(N', P', E', I') around to form a Riemann circle (V, N', P', Ec, Ic), via stereographic projection. There we see clearly the 4 points: "negative unit" N, "positive unit" P, "internal center" I, "external center" E. I & E also have other names: absolutes, limits, boundaries, balance points, fixed points, attractors, extremities.
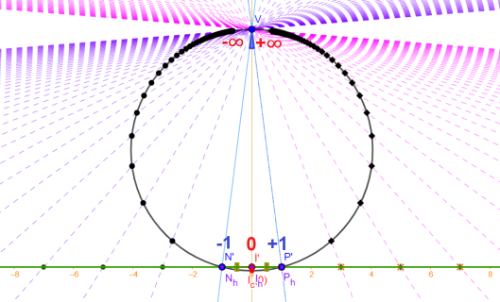
In non-harmonic cases where cross-ratio ≠ -1, we have two other kinds of metrics: exponential metric and growth metric generalizing the linear metric and projective metric in the harmonic case. (In the applet above, uncheck "Harmonic" and choose "Exponential" or "Growth" in the Metric dropdown list). The growth metric is the most general one, which has application in Einstein's Relativity.
The projective & linear metric is just the growth & exponential metric where the two limits (I, E) coincide
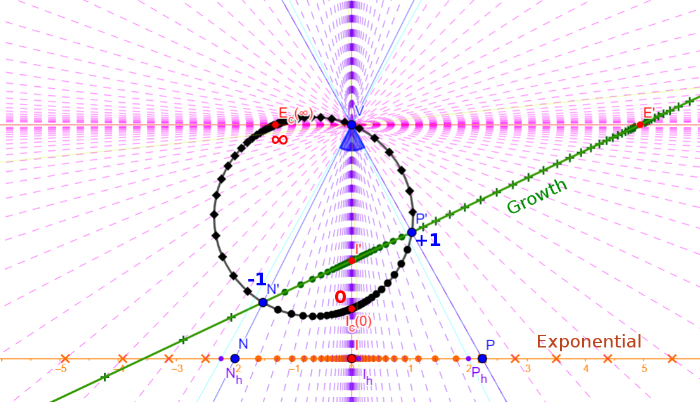
In the following applet, mimicking the case of linear perspective metric, we define a linear metric m() on h using a constant c for the unit pair (N, P) such that m(N)=-c and m(P)=c. Then the measurements of the central pair (E, I), d:=m(I) and e:=m(E), are harmonic conjugates in the sense of inverse geometry: . That's because:
Moreover, we can rewrite the harmonic condition (N, P; E, I) = −1 as a zero sum:
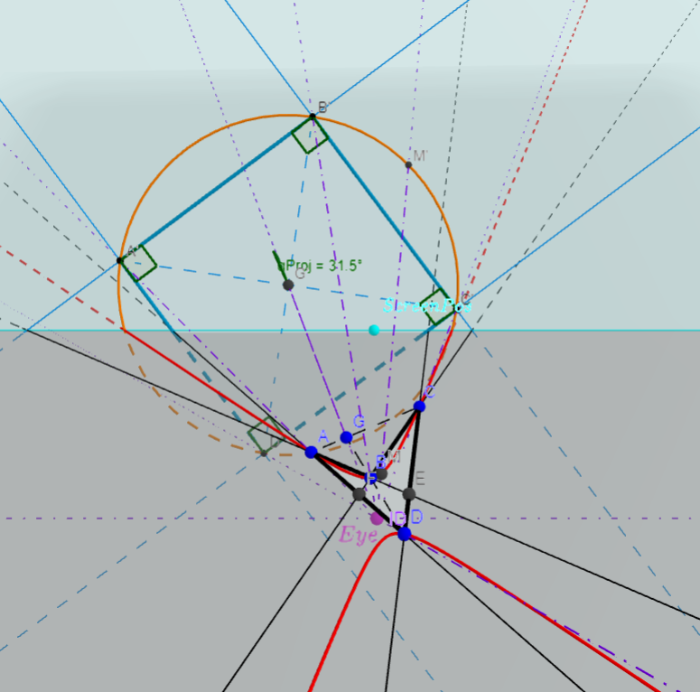
Projective image of Square & Circle
Here, we construct a quadrilateral VTRS (in blue) using an arbitrary point T on VN, and two intersection points R = VI ∩ TP, S = VP ∩ TE. Then R, S are colinear with N. And in reverse, for any quadrilateral RSTV (convex, concave, complex) with three pairs of opposite sides intersect at N = VT ∩ SR, P = VS ∩ TR, Pole = VR ∩ TS, and the line NP intersects with the other two opposite sides at E = NP ∩ VR, I = NP ∩ TS, there are three harmonic quadruples (N, P; E, I), (V, R; I, Pole) and (T, S; E, Pole). Then using a variant of Pascal's theorem, we construct the conic (RSTVUc) circumscribing the quadrilateral RSTV (check "χExtras" to see the point Uc).
Then we can always construct a perspectivity to project that "conic circumscribed quadrilateral" into a "circled square", as shown in this 3D applet. That means any quadrilateral is a projective image of a square as shown in this video, this article, and any conic is a projective image of a circle as shown in the article "Shine a light on Conic sections". So, the line h here is the vanishing line (horizon), and N, P are two vanishing points of the sides of that "square" (square in the object plane).
Moreover, the intersect of two diagonals is the pole and the vanishing line is the polar of the circumscribed conic.