行列式〜連立方程式の鍵
2次行列式の半分
3次行列式の立体化
偶置換のアミダと奇置換のアミダ
1.3次までの行列式
連立方程式の解法のときに、
・余因子行列、
・正則かどうかを知るための計算
・クラメールの公式、
何かと行列式[determinant]の計算が登場しているが、
そもそも、行列式そのものについては、正面からはテーマにしてこなかった。
その理由は、ベクトル、行列、連立方程式、どれもが、
考える対象としても、テーマとしても独立できるほどの広がりがあった。
しかし、行列式は、計算技術という文脈で登場するだけなので、
独立して扱ってこなかった。
しかし、連立方程式を特にも、逆行列の存在を知るにも必要なものなので、
裏方かもしれないが大切なものなので、行列式をここで主役として扱ってみよう。
正方行列に対して、
行列の成分(要素)から取り出した積を作る。
その積に取り出した位置による特性(順列のタイプ)で+かーをつける。
それの総和の値を求める。
その値が行列式。
式の値だから、行列値という方がわかりやすい。
しかし、その計算のための式のルールが大切という意味では行列式というのもわかる。
<2次の行列式>
A={{ a , b},
{ c , d}}
の行列に対する行列式[determinant]は
|A|=ad-bc
det(A)ともかく。
Aの i 行j列目の要素をAijと書くことにすると
行列の位置としてはa11=a, a12=b, a21=c, a22=dだね。
a,b,c,dを使わずに位置記号で書き直そう。
|A|=a11a22- a12a21。
2つの積はa1xa2yという形式になっているので、さらに省略してa1xa2yなら[xy]と書いてみよう。
|A|=[12]-[21]
となっている。結局、1行目→2行目の順に要素を選ぶのは同じで、列の選択が12のままか、
12の交換(互換)1回ありかという順列の問題になっているのがわかるね。
この見方をサラスの方法という。
<2次行列式の図形的な意味>
det(a,b)=列ベクトルa,bを位置ベクトルが張る平行四辺形の面積
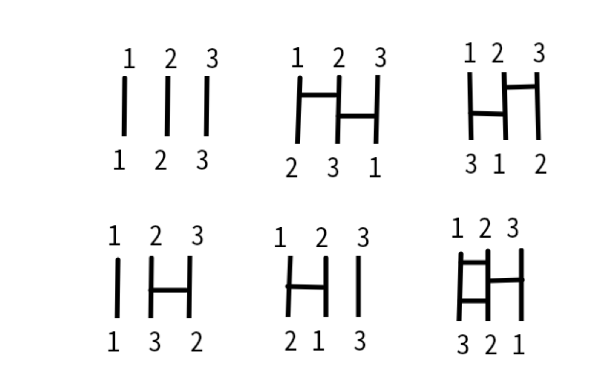
<3次の行列式と置換>
置換というのは順列のことだけど、
なぜ順列と言わないのか?
順列といってしまうと、順列数という、並べ替えの総数という意味で
誤解されるかもしれない。
だから、ただの「並んだもの」という意味で、置換ということがある。
さっきと同じで、上の行から1列ずつ被らないように列数を選んだ積を作ろう。
A={{ a11, a12, a13},
{ a21, a22, a23},
{ a31, a32, a33}}
の行列に対する行列式は、
上から1,2,3行目の要素から選ぶ積a1xa2ya3zを[xyz]と、x列目y列目z列目だけ表示してかくと、
|A|= [123]+[231]+[312] -( [132]+[213]+[321])
+の順列は1⇒2⇒3のサイクリックな仲間になっている。
ーの順列は3⇒2⇒1のサイクリックな仲間になっている。
この見方をサラスの方法という。
サイクリックという用語を使わないで言い換えたのが互換(2つの交換)の個数だ。
[123]に互換を0,2,4,………と偶数回してできる順列を偶置換、
[123]に互換を1,3,5,...... と奇数回してできる順列を奇置換という。
たとえば、[231]は[123]の(12)にアミダの線を入れ、その下に(23)にもアミダの線を入れてみよう。
線のないアミダくじは零置換、恒等置換で無変化だが、
この2本のアミダの線で互換が2回行われる。1の人は3にいき最後へ、2の人は先頭にいったまま。
3の人は1本目の影響はないが、2本目と交換されるから真ん中へ。
だから、[123]は[231]となった。[312]も同様に2本の互換で[123]からできる順列だ。
一方の[213]はどうだろう?[123]の(12)の互換でおしまい。だから置換が1回だから奇置換だね。
これを一般化に近づけると
|A|= ∑ (−1)互換数 [123の順列]
(★ (−1)互換数 は、偶置換なら+1,奇置換なら−1となるね。)
と書けるね。
(一般化)
N次の行列式
|A|=∑(-1)互換数[123...nの順列]
<3次の行列式と余因子>
A={{ a11, a12, a13},
{ a21, a22, a23},
{ a31, a32, a33}}
に対して、Aのi行j列を取り去った行列式に(-1)i+jをかけたものを余因子[cofactor]という。
Aijとかく。
たとえば、A33は
{{ a11, a12},
{ a21, a22},
のように3行と3列が消した行列を作り、
行列式a11a22-a12a21に(-1)3+3=1をかけたものになる。A33=+1(a11a22-a12a21)
第1行による展開例
|A|=a11A11+a12A12+a13A13
= [123]+[231]+[312] -( [132]+[213]+[321])
このように、行を1行に固定してみるとわかるが、i=1のまま、jを1,2,3と変化させると、
符号は+ー+と交互に変化する。
1つ飛ばした余因子は同じ偶置換か奇置換のグループのセットを取り出す。
しかし、1つとなりの列に移動した余因子はサイクリックが狂う。
それでも、狂い方が1行ごとだから、(-1)i+jという符号調整数を込みにした余因子Aijだから、
この符号調整を忘れなければ、記述が非常にカンタンになる点がよいね。
<行列式の図形的な意味>
3つの列ベクトルa={a1,a2,a3},b={b1,b2,b3},c={c1,c2,c3}の行列式det(a,b,c)を求める。
A={{ a1, b1, c1},
{ a2, b2, c2},
{ a3, b3, c3}}とすると、
c列による展開
det(A)=c1A13+c2A23+c3A33
=(a✕b)・c
=|| a✕b || || c || cosφ
この絶対値※は、
(aとbが張る平行四辺形の面積)・(a,b,cが張る平行6面体の高さ)
a,b,cが張る平行6面体の体積。
(※外積はaからbへの右ネジ向きにできるベクトルだから、それが、ベクトルcの向きと
反対向きだと、内積が負になることがあるので、絶対値にする。)
2.N次の行列式
前記の内容がわかれば、
すぐに一般化できるね。
<互換数での一般化>
123....nの順列(置換)をPとする。
Pの互換数をQとしよう。
sgn(P)=(-1)Q
順列Pが偶置換なら+をつけ、奇置換ならーをつけて総和を求める。
それがsgn(P)の意味。
|A|=∑sgn(P)[P]
<余因子での一般化>
kは行数または列数の定数
|A|=∑akjAki または、|A|=∑aikAik。
<行列式の簡約法則>
あまり一般化しすぎると意味があいまいになったり混乱の原因になることがある。
そこで、5次の行列式として一般法則をさぐろう。
同じ列の要素を列ベクトルのようにみなし省略して行番号だけを表記する。
A=
{{ a11, a12, a13, a14, a15},
{ a21, a22, a23, a24, a25},
{ a31, a32, a33, a34, a35},
{ a41, a42, a43, a44, a55},
{ a51, a52, a53, a54, a55}}
a1=
{{ a11},
{ a21},
{ a31},
{ a41},
{ a51}}
と書くと、
A={a1,a2,a3,a4,a5}
となる。
a1=
{{ b11+c11},
{ b21+c21},
{ b31+c31},
{ b41+c41},
{ b51+c51}}
とa1が分割できたらどうなるだろう。
a1=b1+c1
和の行列式は、行列式の和
det(a1,a2,a3,a4,a5)=det(b1+c1,a2,a3,a4,a5)=det(b1,a2,a3,a4,a)+det(c1,a2,a3,a4,a5)
(理由)
a1列のどの行の要素もb1とc1に分解できる。
すると、互換数の式で考えると、偶置換の順列式も奇置換の順列式でもax1=bx1+cx1と分割される。
だから、どの順列も互換数の符号はまったくそのままでax1をbx1に置き換えた式と
ax1をcx1に置き換えた式ができるね。
もっとカンタンに変更のある列だけ書くとこうなる。
・|b1+c1,・・・・| = |b1,・・・・| + |c1,・・・・|
つまり、線形性の1つ<和の法則>=0が成り立つね。
・線形性といえば、<定数倍の法則>もある。
定数倍の行列式は、行列式の定数倍
|c b1,・・・・| = c |b1,・・・・|
(理由)
a1=b1+b1+b1とすると、和の法則から、
|3b1,・・・・| = |b1+b1+b1,・・・・| = 3|b1,・・・・|
のようにして、個数を増やしていけるから。
・A={a1,・,a3,・・}とB={a3,・,a1,・・}のように、
2つの列を入れ替えると、符号が反対になる。det(A)=-det(B)
<交代性>という。
(理由)
Aの順列が[12345]に対して[31245]のように、2つの列の互換の順列になるから、
偶置換と奇置換が入れ替わるので、すべての順列が反対の符号になるから。
|a1,・,a3,・・| = -|a3,・,a1,・・|
・A={a1,・,a1,・・}と同じ列があるとde(A)=0
(理由)
|a1,・,a1,・・|=xとして、2つの列を入れ替えると、符号が反対になるから、
|a1,・,a1,・・|=‐x
両辺の和から、|a1,・,a1,・・|=0
・|a1,・,a3,・・|=|a1,・,a3 ± ka1 ,・・|と他の列の定数倍の和差をしても行列式の値は不変
(理由)|a1,・,a3 ± ka1 ,・・| = |a1,・,a3,・・| ± k |a1,・, a1 ,・・|
=|a1,・,a3,・・| ± 0
だから。
この最後の、「別の行に行の定数倍の足し算してOK」というのが、とても便利だ。
・転置不変(det(tA)=det(A))
・積の行列式は行列式の積(det(AB)=det(A)det(B))
3.演習
<行列式の値>
・単位行列式の値は1。
E={{ 1, 0, 0},
{ 0, 1, 0},
{ 0, 0, 1}}
det(E)=1(1・1-0・0)=13=0
・三角行列。対角成分の下が零の行列の行列式は対角成分の積になる。
D1={{ a, x, y},
{ 0, b, z},
{ 0, 0, c}}
1列目で展開して余因子で表すと、D11のみ残る。これを次元が上がっても繰り返す。
det(D1)=aD11+0D21+0D31=aD11
D2={{ b, z},
{ 0, c}}
D11=det(D2)=bc-0=bc。以上から、det(D1)=abc。
(例)det(A)は?
A={{ 6, 0, 5 },
{ 3, 2, 2},
{ 1, 4, 1}}
余因子で展開する。
1行目で展開する。
det(A)=6A11+0A12+5A13
=6(2-8)+0+5(12-2)=-36+50=-14
(例)det(A1)は?
A1={{ λ+3, λ , 1 },
{ 1, 2λ+2, 1},
{ 1, λ, λ+3}}
他の行・列の定数倍を加減してから、余因子で展開する。
各行の和が一定の2λ+4だから、2列目と3列目を1列目にたしても値は不変。
A2={{ 2λ+4, λ , 1 },
{ 2λ+4, 2λ+2, 1 },
{ 2λ+4, λ, λ+3 }}
1列目の2λ+4を定数として行列式の外に出す。
A2=(2λ+4){{1, λ , 1 },
{1,2λ+2, 1 },
{1 , λ, λ+3 }}
1列目を3列目からひき、1列目のλ倍を2列目から引く。
A3=2(λ+2){{1, 0, 0},
{1, λ+2, 0 },
{1 , 0, λ+2 }}
det(A3)=det(A2)=det(A1)=3(λ+2){1(λ+2)2-0)}=3(λ+2)3
(例)det(A1)は?
A1={{ 2x, x ,x, x },
{ x, 2x, x, x },
{ x, x, 2x, x },
{ x, x, x, 2x }}
他の行・列の定数倍を加減してから、余因子で展開する。
xを定数とみなして行列の外に出す。
A2=x4{{ 2, 1 ,1, 1 },
{ 1, 2, 1, 1 },
{ 1, 1, 2, 1 },
{ 1, 1, 1, 2 }}
各行の和が5で一定なので、2,3,4行目を1行目にたす。
A3=x4{{ 5, 1 ,1, 1 },
{ 5, 2, 1, 1 },
{ 5, 1, 2, 1 },
{ 5, 1, 1, 2 }}
1列目の定数を外に出す。
A4=5x4{{ 1, 1 ,1, 1 },
{ 1, 2, 1, 1 },
{ 1, 1, 2, 1 },
{ 1, 1, 1, 2 }}
1列目を2,3,4列目からひく。
A4=5x4{{ 1, 0 ,0, 0 },
{ 1, 1, 0, 0 },
{ 1, 0, 1, 0 },
{ 1, 0, 0, 1 }}
2,3,4列目を1列目からひく。
A4=5x4{{ 1, 0 ,0, 0 },
{ 0, 1, 0, 0 },
{ 0, 0, 1, 0 },
{ 0, 0, 0, 1 }}
det(A4)=det(A1)=5x4(14)=5x4