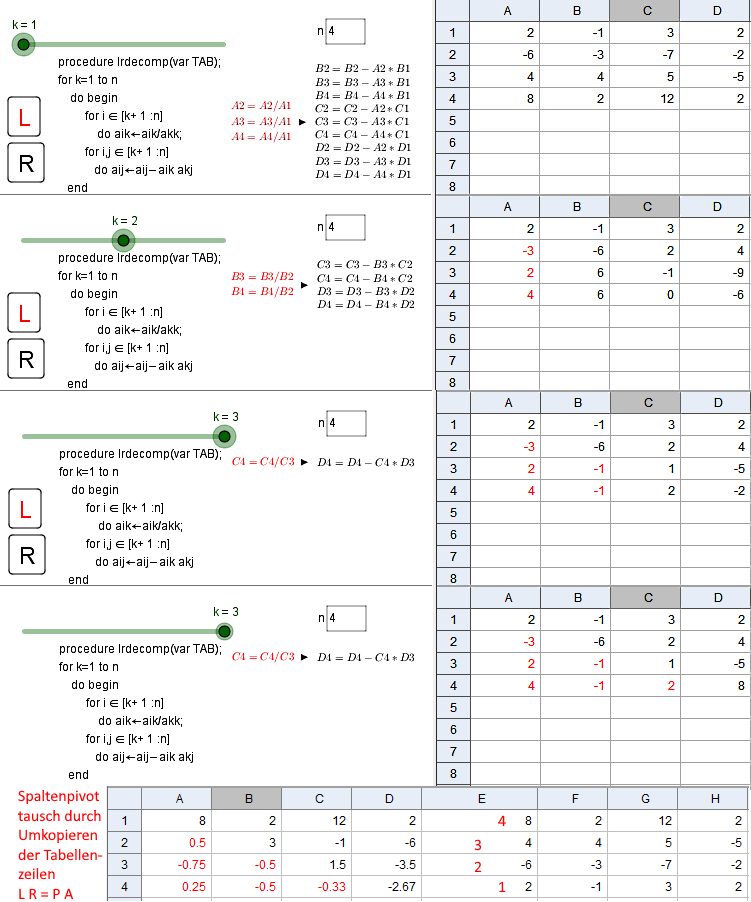
LR Zerlegung auf einem Matrixfeld
Dieses Beispiel ist dem Algorithmus die LR Zerlegung auf einem Matrixfeld durchzuführen nach empfunden.
Die Faktoren für die Gaußelimination werden gebildet aus der 1.Spalte dividiert durch Diagonalelement der jeweiligen (Rest)Matrix:
Im 1.Schritt {{a11,a21,a31,a41}}/a11, dieser Vektor bildet die 1.Spalte der L-Matrix und mit geänderten Vorzeichen unter dem Diagonalelement die 1. Spalte der Gaußeliminationsmatrix Li .
(etwa Sequence(Sequence({c(i,j) , a(i,j) - a(k,j) a(i,k) / a(k,k) }, i,k+1,n), j,k+1,n);
spaltenweise berechnung - LRdecomp() zeilenweise wg. matrixaufbau im cas;
In die 0 Elemente der 1.Spalte L1 A werden die entsprechenden Elemente des Faktorvektors geschrieben.
Mit der Untermatrix ( cij )von L1 A wird entsprechend dem 1.Schritt weiter gearbeitet
(aij) ==> (cij) ==> (uij) ==> u'44
In der App speichere ich den Status nach jedem Schritt in den Matrizen Ai . Zum Schluss zerlege ich das Matrixfeld LR in die Matrizen L R . ggb-CAS bedingt muss für jeden Schritt eine Matrix angelegt werden!
Die user-function LRdecomp() setzt den oben beschrieben Algorithmus um. Die Pivottauschmatrizen können einfach auf die Matrixfelder Ai angewendet werden - Pi Matrizen für die Zeilenpivotsuche (user-function SPivot() sind vorhanden. Für Spaltenpivotsuche können sie einfach Pi, Qi Matrizen dazuschreiben. Zeile
(29) {L R ,P3 P2 P1 A Q1 Q2 Q3} anpassen .
Besser zu "sehen" ist der Algorithmus - Prozedurale Programmschritte - in der folgenden App - Pseudoprogramm und Script - allerdings nicht im CAS - achten Sie auf Rundungsfehler....
LRdecomp(AA,kk):=Join(Take(AA,1,kk),Sequence(Flatten({If(kk>1,Take(Element(AA,i),1,kk-1),{}),Element(AA, i,kk)/Element(AA, kk,kk),Sequence(Element(AA,i,j) - Element(AA,kk,j) Element(AA,i,kk) / Element(AA,kk,kk) , j,kk+1,n)}), i,kk+1,n));
Lesen des Matrixfeldes nach einem Gauß-Schritt
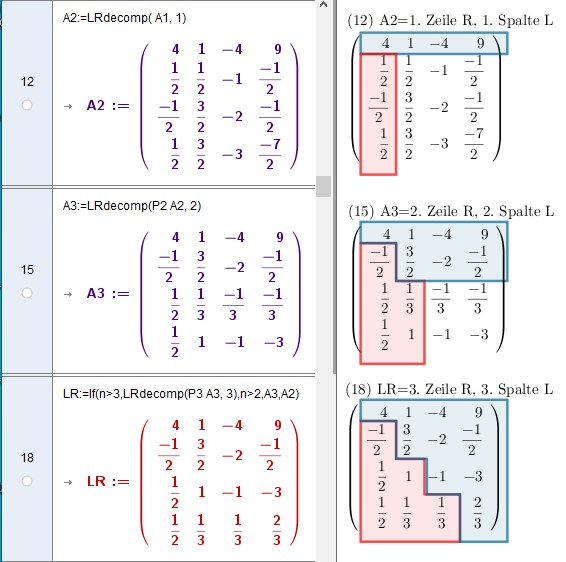
LRimMatrixfeldR4
Prozedurale Programmschritte