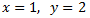Sistemes d'Equacions: Substitució, igualació i reducció
Introducció
Un sistema d'equacions és un conjunt d'equacions amb diverses incògnites. Les incògnites poden aparèixer o no en totes les equacions. Per exemple,
 Per resoldre el sistema tenim que obtenir els valors de les incògnites que fan que es compleixin totes les equacions alhora.
Nosoltres anem a resoldre aquest sistema de dues equacions i dues incògnites pels tres mètodes bàsics: substitució, igualació i reducció.
Per resoldre el sistema tenim que obtenir els valors de les incògnites que fan que es compleixin totes les equacions alhora.
Nosoltres anem a resoldre aquest sistema de dues equacions i dues incògnites pels tres mètodes bàsics: substitució, igualació i reducció.
 Per resoldre el sistema tenim que obtenir els valors de les incògnites que fan que es compleixin totes les equacions alhora.
Nosoltres anem a resoldre aquest sistema de dues equacions i dues incògnites pels tres mètodes bàsics: substitució, igualació i reducció.
Per resoldre el sistema tenim que obtenir els valors de les incògnites que fan que es compleixin totes les equacions alhora.
Nosoltres anem a resoldre aquest sistema de dues equacions i dues incògnites pels tres mètodes bàsics: substitució, igualació i reducció.
1. Mètode de Substitució
Aquest mètode consisteix en aïllar una de les dues incògnites, per exemple la , en una de les equacions i substituir aquesta expressió en l'altra equació. D'aquesta manera, obtindrem una equació de primer grau.
En l'exemple

Aïllem la en la primera equació:
Aïllem la en la primera equació:
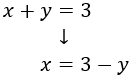
Ara, en la segona equació, escrivim aquesta expressió on aparegui la i resolem l'equació:
Ara, en la segona equació, escrivim aquesta expressió on aparegui la i resolem l'equació:
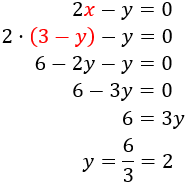
Ara, sabent el valor de , podem calcular la :
Ara, sabent el valor de , podem calcular la :
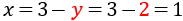 Per tant, la solució del sistema és
Per tant, la solució del sistema és
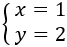

Aïllem la en la primera equació:
Aïllem la en la primera equació:
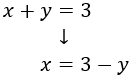
Ara, en la segona equació, escrivim aquesta expressió on aparegui la i resolem l'equació:
Ara, en la segona equació, escrivim aquesta expressió on aparegui la i resolem l'equació:
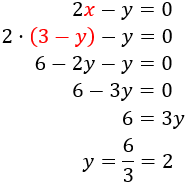
Ara, sabent el valor de , podem calcular la :
Ara, sabent el valor de , podem calcular la :
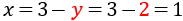 Per tant, la solució del sistema és
Per tant, la solució del sistema és
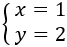
2. Mètode d'Igualació
En aquest mètode, el que fem és aïllar una de les incògnites en les dues equacions per tal d'igualar ambdues expressions. Així obtenim una equació de primer grau:
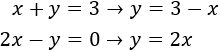
Igualem:
Igualem:
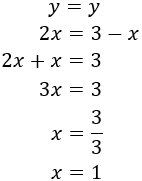
Ara podem calcular l'altra incògnita:
Ara podem calcular l'altra incògnita:
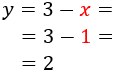
Per tant, la solució del sistema és:
Per tant, la solució del sistema és:
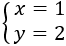
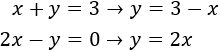
Igualem:
Igualem:
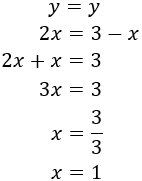
Ara podem calcular l'altra incògnita:
Ara podem calcular l'altra incògnita:
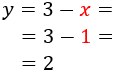
Per tant, la solució del sistema és:
Per tant, la solució del sistema és:
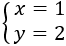
3. Mêtode de Reducció
Realitzem operacions entre les dues equacions per aconseguir que una de les incògnites desaparegui. Aleshores tindrem una equació de primer grau:
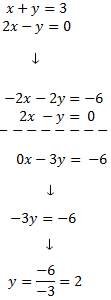
Calculem :
Calculem :
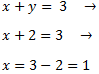
Per tant, la solució del sistema és
Per tant, la solució del sistema és
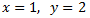
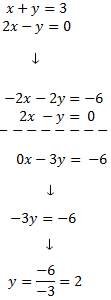
Calculem :
Calculem :
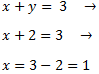
Per tant, la solució del sistema és
Per tant, la solució del sistema és