Paradoxon von Bertrand
Wie groß ist die Wahrscheinlichkeit, dass eine zufällig ausgewählte Sehne des Einheitskreises länger als eine Seite eines in diesen Kreis eingeschriebenen gleichseitigen Dreiecks ist?
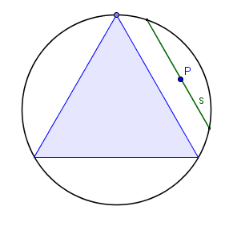
Variante 1
Jede Sehne lässt sich eindeutig durch ihren Mittelpunkt angeben (die Sehne wird dann normal zur Verbindungslinie mit dem Kreismittelpunkt gebildet).
Der Mittelpunkt P der Sehne wird durch die kartesischen Koordinaten (x,y) angegeben.
Der Ereignisraum Ω1 ist auf diese Weise durch gegeben.
Ereignis A1: Die gewählte Sehne ist größer als die Dreiecksseite;
Die Wahrscheinlichkeit für A1 beträgt .
Aufgabe
Bewege den Punkt P und die obere Spitze des Dreiecks, um dich mit der Problemstellung vertraut zu machen.
Zeige die Simulation an.
Variante 2
Der Mittelpunkt der Sehne kann auch durch seine Polarkoordinaten (r; φ) angegeben werden.
Der Ereignisraum Ω2 ist auf diese Weise durch gegeben.
Ereignis A2: Die gewählte Sehne ist größer als die Dreiecksseite;
Die Wahrscheinlichkeit für A2 beträgt .
Aufgabe
Bewege den Punkt P und die obere Spitze des Dreiecks.
Zeige die Simulation an.
Variante 3
Die Sehne kann auch durch einen Punkt am Rand des Kreises (d. h. durch die Bogenlänge b) und einem Winkel α zur Tangente angegeben werden.
Der Ereignisraum Ω3 ist auf diese Weise durch gegeben.
Ereignis A3: Die gewählte Sehne ist größer als die Dreiecksseite;
Die Wahrscheinlichkeit für A3 beträgt .
Aufgabe
Bewege den Punkt P und die obere Spitze des Dreiecks sowie den Schieberegler für den Winkel α.
Zeige die Simulation an.
Das Paradoxon besteht darin, dass es - je nach Wahl der Sehne - verschiedene Wahrscheinlichkeiten gibt.
Die Ursache liegt dabei in der Tatsache, dass die zufällige Auswahl einer Sehne nicht genau vorgegeben wird.