L6.13 - Intersection Points
Learning Intentions and Success Criteria
- Use graphical methods to solve a system of equations consisting of one linear and one quadratic equation.
- Use a graph to find the intersection points of a line and a circle.
13.1: Which One Doesn’t Belong: Lines and Curves
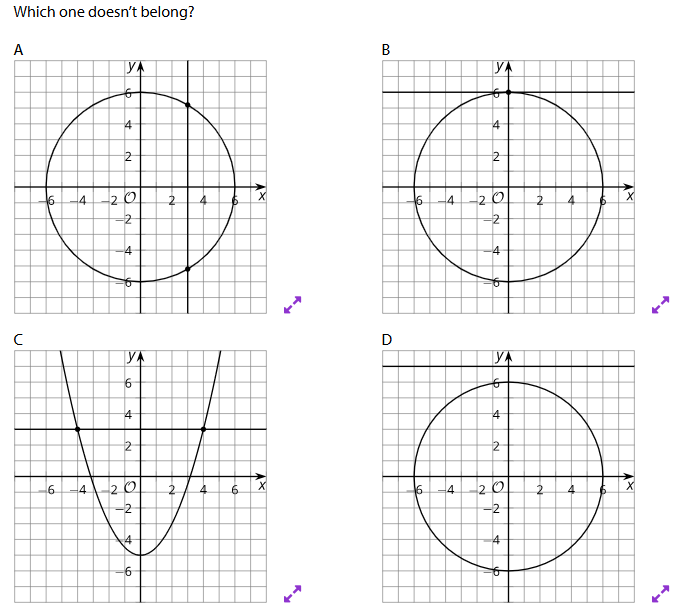
Which one doesn't belong? Explain why.
13.2: Circles and Lines
1. The equation (x - 3) + (y - 2) = 25 represents a circle. Graph this circle on the coordinate grid. 2. Graph the line y = 6. At what points does this line appear to intersect the circle?
3. How can you verify that the 2 figures really intersect at these points? Carry out whatever procedure you decide.
4. Graph the line y = x - 2. At what points does this line appear to intersect the circle? Verify that the 2 figures really do intersect at these points.
13.3: Creating Lines
1. Write an equation representing the circle in the graph.
a. any line parallel to the x-axis that intersects the circle at 2 points
b. any line perpendicular to the x-axis that doesn’t intersect the circle
c. the line perpendicular to y = x + 5 that intersects the circle at (6, 8)
3. For the last line you graphed, find the second point where the line intersects the circle. Explain or show your reasoning.
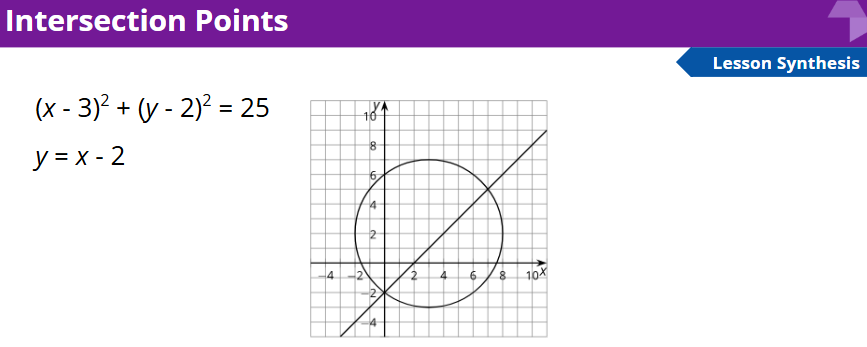
What does each equation represent on the graph?
What is special about the point (7, 5) on the graph?
What is special about the point (7, 5) with regard to the equations?
Learning Intentions and Success Criteria
- Use graphical methods to solve a system of equations consisting of one linear and one quadratic equation.
- Use a graph to find the intersection points of a line and a circle.
Cool-down: Find and Verify
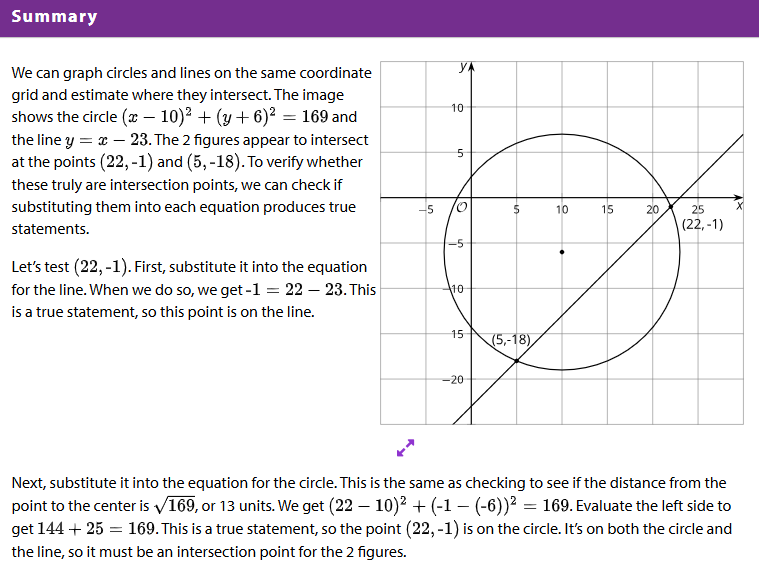
The image shows the graph of (x - 5) + (y + 1) = 25. 1. Graph the line y = x - 5. 2. At how many points does this line intersect the circle?
3. Find and verify at least one point where the circle and line intersect.


