1.1 Definições
Considerando um polígono convexo ABCD ... MN contido em um plano α e um ponto V fora de α. Chamamos de pirâmide, à reunião dos segmentos definidos pelo ponto V e pelos vértices do polígono (Dolce, 2013, p.178).
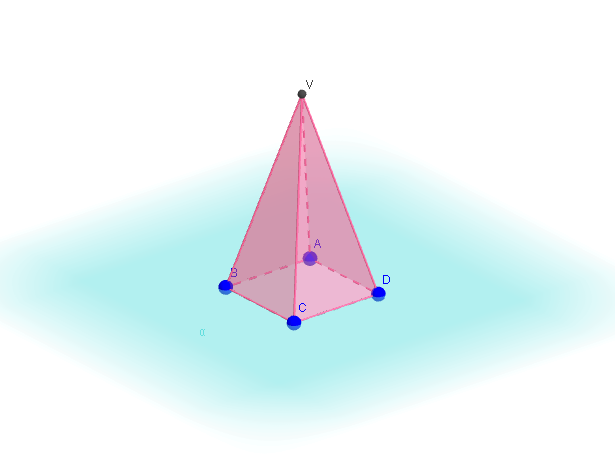
Uma pirâmide qualquer possui os seguintes elementos:
- Uma base (determinada pelo polígono convexo);
- N faces laterais (todas representam triângulos);
- N + 1 faces (referente às laterais mais a base);
- N + 1 vértices (correspondentes aos vértices do polígono da base mais o ponto V, que encontra-se fora do plano da base);
- 2N arestas;
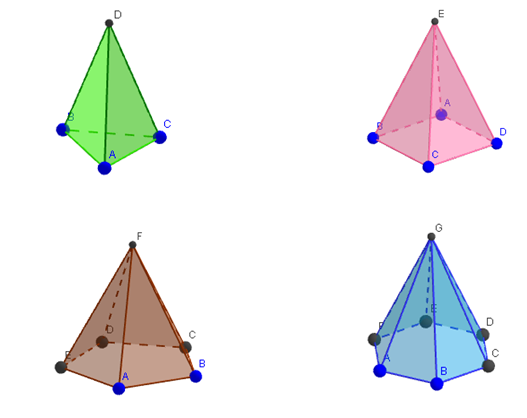
Além dessa classificação, as pirâmides podem ser retas ou oblíquas. Além de serem retas, podem ser regulares, que caracterizam-se por possuir a projeção ortogonal do vértice sobre o plano da base, tornando-se o centro da mesma. Além disso, em uma pirâmide regular, as arestas laterais são congruentes e as faces são triângulos isósceles congruentes. Dentre os elementos já apontados, a pirâmide apresenta um apótema, que pode ser da base, ou da própria pirâmide. O apótema da pirâmide (AP) representa a altura da face lateral, enquanto o apótema da base (ap) é dado pelo raio da circunferência inscrita no polígono da base, conforme segue na figura abaixo.
- A altura (h) é a distância entre o vértice e o plano da base.
- Portanto, podemos determiná-las por Pitágoras, a partir da relação:
AP² = ap ² + h²