Paridad de funciones

作成者:JLF

トピック:関数

Una función

de variable real

Ejemplos: La función f(x) = x^2 es par:

La función f(x) = x^3 es impar:

Propiedades

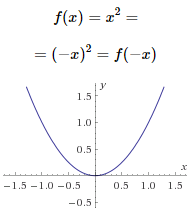
La gráfica de una función par presenta simetría respecto del eje de las ordenadas.
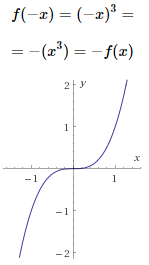
La gráfica de una función impar presenta simetría rotacional (rotación de 180 grados).
La función constante f(x) = k es par.
La suma de funciones pares es una función par.
La suma de funciones impares es impar.
El producto de dos funciones pares es una función par.
El producto de dos funciones impares es una función par.
La derivada de una función par es una función impar.
La derivada de una función impar es una función par.
La composición de dos funciones pares es una función par.
La composición de dos funciones impares es una función impar.
Toda función definida sobre los reales puede escribirse como la suma de una función par y una función impar.