Outline
Archimedes' Method of Finding π
- Author:
- brentsiegrist
- Topic:
- Circle
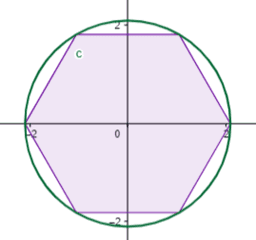
Archimedes estimated the circumference of a circle by inscribing a regular polygon. All the sides and angles of a regular polygon are congruent. An inscribed polygon touches the circle at its vertices. Since each side of the inscribed polygon was shorter than the arc of the circle beside it, the perimeter of the inscribed polygon was shorter than the circumference of the circle. He divided this number by the diameter of the circle to get a minimum value for π.
Archimedes then estimated the circumference of a circle by circumscribing a regular polygon. A circumscribed polygon touches the circle at the midpoint of each side. Since each side of the circumscribed polygon was longer than the arc of the circle beside it, the perimeter of the circumscribed polygon was longer than the circumference of the circle. He divided this number by the diameter of the circle to get a maximum value for π.
As Archimedes increase the number of sides of his polygons, his minimum value for π increased, and his maximum value for π decreased, until they were almost the same. His largest polygons has 96 sides. He averaged their perimeters to make his final estimate of π.
Archimedes lived several hundred years before Jesus. His estimate of π was more accurate than estimates made by the ancient Egyptians and Babylonians, and it was used for hundreds of years. Mathematicians found ways of estimating π that are more efficient but hard to explain. The invention of computers made it possible to calculate it to millions of decimal places. But Archimedes' estimate of 3.14 or 22/7 continues to be good enough for most ordinary calculations.
