Einführung Rotationskörper
Definition Rotationskörper
Ausgangslage: Wir betrachten den Graphen einer Funktion f. Diesen Graphen drehen wir nun um die x-Achse. Während der Drehung nehmen wir die Lage des Graphen durch "Schnappschüsse" auf (stop motion) und legen diese anschließend übereinander. Wir erkennen, dass die Graphen einen Körper bilden.
Beispiel 1
Beispiel 2
Bestimmung des Volumens eines Rotationskörpers
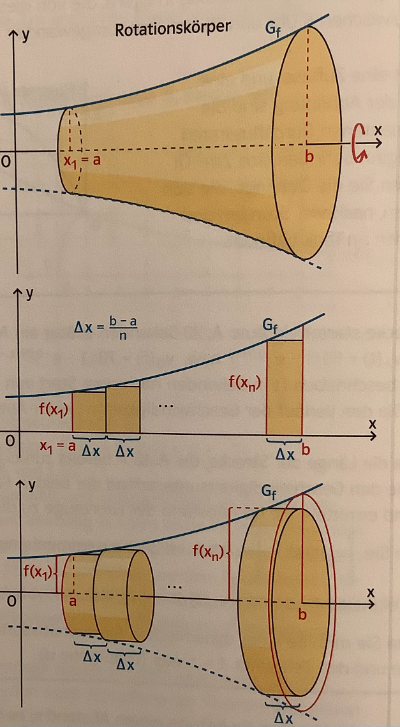
Entsteht ein Rotationskörper durch Drehung eines Graphs um die x-Achse lässt sich sein Volumen analog zur Streifenmethode bei der Flächenberechnung ermitteln.
| Flächenberechnung | Volumenberechnung | |
| Methode | Auslegen der Fläche durch unendlich viele unendlich dünne Rechtecksstreifen | Auslegen der Raumes durch unendlich viele unendlich dünne Zylinderscheiben |
| Maß | Rechtecksfläche | Zylindervolumen |
| Summierung | Integral | Integral |
Veranschaulichung