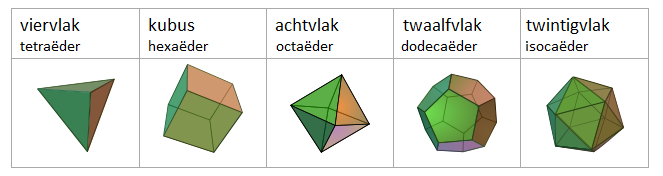
Platonische lichamen
Pythagoras (6e eeuw v.Chr.) zag in Egypte de piramides en in Zuid-Italië de twaalfvlakkige dobbelstenen die de Romeinen gebruikten. Hij geloofde dat de werkelijkheid kon begrepen worden door hun wiskundige samenhang te onderzoeken en kende driehoeken en vijfhoeken spirituele betekenis toe.
Een eeuw na zijn dood onderzoekt Plato hoeveel mogelijke regelmatige veelvlakken er mogelijk zijn.
Samen met zijn vriend Thaetetus legt hij de voorwaarden voor zo'n regelmatigheid vast.
Een regelmatig veelvlak is een convex veelvlak waarvan de zijvlakken congruente regelmatige veelhoeken zijn. en ook alle hoekpunten congruent zijn..
Ze besluiten:
- De zijvlakken kunnen hoogstens regelmatige vijfhoeken zijn.
- Er zijn slechts vijf mogelijke regelmatige veelvlakken.
We noemen ze 'de vijf Platonische lichamen'.
Wat zijn de voorwaarden voor een regelmatig veelvlak:
- De zijvlakken zijn regelmatig (gelijkzijdige driehoek, vierkant of gelijkzijdige vijfhoek)
Met regelmatige zeshoeken, zeven- of meerhoeken kan je geen lichaam vormen.
- De zijvlakken zijn congruent
- De hoekpunten zijn congruent
- Het veelvlak is convex (anders gezegd: er zitten geen holtes in).
Met deze voorwaarden komen we tot vijf regelmatige veelvlakken: