Rosace Quadrilobée
Je pars de 2 points A et B, sur lesquels je construis un carré via 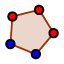 2 points sont créés C et D.
Je trace la diagonale [BD] via
2 points sont créés C et D.
Je trace la diagonale [BD] via 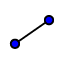 et la bissectrice de via
et la bissectrice de via 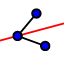 . Cette dernière a le point E comme intersection avec [BC]
. Cette dernière a le point E comme intersection avec [BC]  .
Je construis alors le cercle de centre E passant par C via
.
Je construis alors le cercle de centre E passant par C via 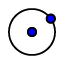 et je détermine son point de tangence F avec [DB] via
et je détermine son point de tangence F avec [DB] via  . Je crée le symétrique F' de F par rapport à [BC] via
. Je crée le symétrique F' de F par rapport à [BC] via  .
Je construis l'arc de cercle via
.
Je construis l'arc de cercle via  , puis je crée le symétrique F'' de F' par rapport à [BD] et l'arc de cercle . Je termine la figure en construisant les symétriques des 2 arcs par rapport au point B via
, puis je crée le symétrique F'' de F' par rapport à [BD] et l'arc de cercle . Je termine la figure en construisant les symétriques des 2 arcs par rapport au point B via 
 2 points sont créés C et D.
Je trace la diagonale [BD] via
2 points sont créés C et D.
Je trace la diagonale [BD] via  et la bissectrice de via
et la bissectrice de via  . Cette dernière a le point E comme intersection avec [BC]
. Cette dernière a le point E comme intersection avec [BC]  .
Je construis alors le cercle de centre E passant par C via
.
Je construis alors le cercle de centre E passant par C via  et je détermine son point de tangence F avec [DB] via
et je détermine son point de tangence F avec [DB] via  . Je crée le symétrique F' de F par rapport à [BC] via
. Je crée le symétrique F' de F par rapport à [BC] via  .
Je construis l'arc de cercle via
.
Je construis l'arc de cercle via  , puis je crée le symétrique F'' de F' par rapport à [BD] et l'arc de cercle . Je termine la figure en construisant les symétriques des 2 arcs par rapport au point B via
, puis je crée le symétrique F'' de F' par rapport à [BD] et l'arc de cercle . Je termine la figure en construisant les symétriques des 2 arcs par rapport au point B via 
Oui, pour le 2ème arc j'aurais pu utiliser une symétrie par rapport à [BD]