ER - Rechnen mit Vektoren (2-dimensional)
Erarbeitung
Arbeite sorgfältig und gewissenhaft die Aufgaben durch. Für deinen Aufschrieb bist du selbst verantwortlich, notiere dir also Ergebnisse und/oder die exemplarischen Rechnungen eigenständig auf dem Arbeitsblatt
Zu Herausforderung 1:
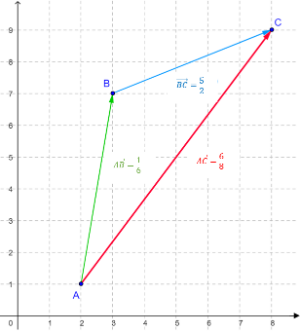
Herausforderung 1a
Welche Rechenoperation wird hier geometrisch dargestellt?
Herausforderung 1b
Wie kann dies geometrisch interpretiert werden?
Herausforderung 1c
Formuliere eine Formel für die Rechenoperation:
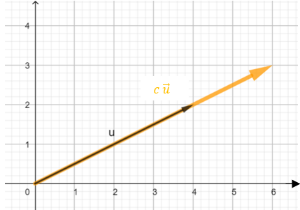
Herausforderung 2a
Welche Rechenoperation wird hier geometrisch dargestellt?
Herausforderung 2b
Wie kann dies geometrisch interpretiert werden?
Herausforderung 2c
Formuliere eine Formel für die Rechenoperation:
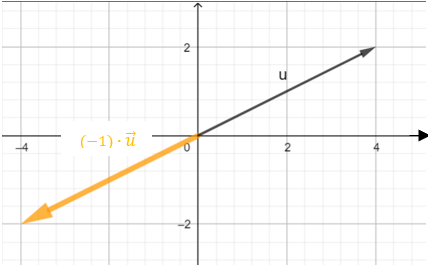
Herausforderung 2c
Welche Rechenoperation wird hier geometrisch dargestellt?
Herausforderung 2d
Wie kann dies geometrisch interpretiert werden?
Herausforderung 3
Aufgabe zu Herausforderung 3
Die Vektoren und werden mit den Koeffizienten und multipliziert. Durch Addition ergibt sich der Vektor . 1. Passe die Koeffizienten so an, dass der Vektor = beträgt. 2. Eine solche Verbindung von Addition und Skalarmultiplikation nennt man ___________________________ . (Fülle die Lücke)
Rechenregeln
Für die Vektoraddition und die Skalarmultiplikation gelten einige Rechenreglen, wie man sie schon vom Rechnen mit reelen Zahlen her kennt --> siehe Buch S. 196
Herausforderung 4
Gilt für zwei Vektoren und der Zusammenhang =, sagt man: und sind kollinear.
Giltf für mehrere Vektoren , und der Zusammenhang , sagt man: und sind linear abhängig.
Aufgabe zu Herausforderung 4
Welche Aussagen sind nicht korrekt?