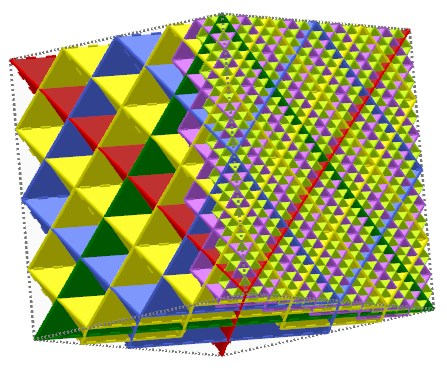
Koch's snowflake fractal 3D (Tetrahedron-Cube)
Das räumliche Analogon zur Koch-Kurve kann als ein Tetraederfraktal aufgefasst werden.
Die vier Seitenflächen eines regulären Tetraeders werden durch Halbieren der Kanten in vier gleichseitige Dreiecke geteilt über denen neue Tetraeder errichtet werden. Die Seitenhalbierung wird über alle Tetraeder weitergeführt. In der ersten Iterationsstufe entsteht der Kepplerstern. Die acht Ecken der Stella Octangula sind die Ecken eines Würfels. Das Tetraederfraktal (unendlich viele Halbierungen) füllt das Würfel-Volumen aus.
5 Iterationsschritte (4,5 nur teilweise dargestellt)
0 - Tetraeder Grün
1 - Tetaeder Rot
2 - Tetraeder (8) blau
3 - Tetraeder 8x8 gelb
4 - Tetraeder Violet 16 Blöcke a 8 (Rest ausgelassen)
5 - Tetraeder hellgrün
Auf der Unterseite sieht man das Aufbaumuster aller Iterationsschritte nebeneinander (gleichzeitig):
aus Mathematische Modelle
KochSnowflakeTetraederStern
Konstruktionsprinzip (Algorithmus)
| | Ich erzeuge aus dem Ausgangstetraeder einen Tetraeder dessen Kantenmitten auf den halbierten Kanten des Ausgangstetraeder liegen. |
| | Der 2. Iterationsschritt geht über die Kantenmitten des (Um)Kubus und generiert 8 Tetraeder mit der Grundfläche 3er benachbarter Kantenmitten des Umkubus (unter jeder Ecke des Umkubus) Es entsteht ein Kuboktaeder. |
| | Jeder weitere Schritt beginnt in einem Kubus mit halbierten Kanten des Vorgänger-Kubus. in dem die Konstruktion von Schritt 2 wiederholt wird. |
| | Im Schritt 3 wird je ein Koboktateder-Block (Würfel) in den 4 Teilwürfeln des Grundcubus erzeugt. In der App durch Drehungen, Verschiebungen kopiert. |
| | dito Schritt 4 benötigt 4^3 Koboktateder-Blöcke |
| | Zusammenstellung mit je einem Block aus Schritt 3 und Schritt 4 |
Iteration Step 5