Heatmap behind a single slit, represented as a system of point sources of damped waves./Heatmap hinter einem Einzelspalt, die als System von Punktquellen gedämpfter Wellen dargestellt wird.
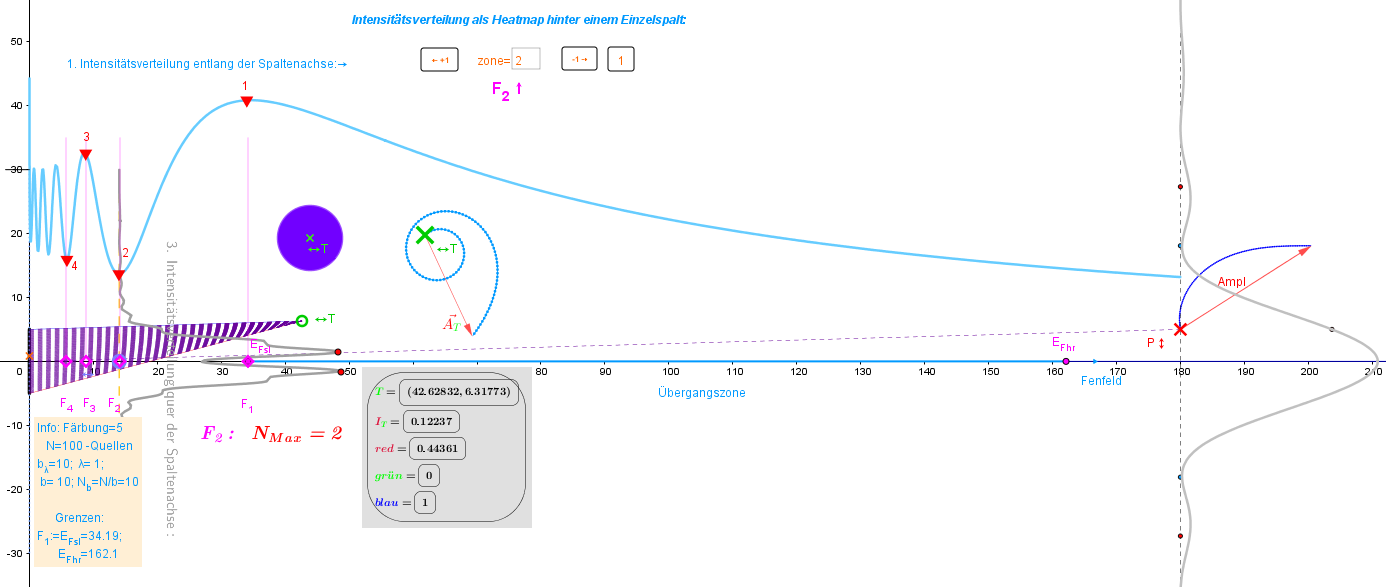
● Simulation der Wellenausbreitung durch die Huygens-Fresnel-Methode. Der optischer Spalt wird durch ein System von Elementarwellenquellen ersetzt. Anzahl der Sender NQ kann variieren. Mit dem Superpositionsprinzip und der Vektordiagrammmethode wird das entstehende Feld des Interferenzmusters berechnet.
● Berücksichtigung der Änderung des Feld des Elementaremitters.
Ausgehend von der Physik des Beugungsphänomens es offensichtlich, dass die Intensität des Lichtfeldes im Nahfeldbereich um eines bestimmten Wertes oszillieren sollte. In einer beträchtlichen Spaltabstand sollte die Intensität asymptotisch gegen dieses bestimmten Wert abnehmen. Dieses Verhalten der Intensität der Schwingungen kann erhalten werden, wenn die Abnahme der Amplitude mit dem Abstand r: 1/ sqrt (r) für das eindimensionale und 1/ r- für zweidimensionale Modelle sind.
● Längs- und Querachse Intensitätsverteilungen bei der Beugung am Einzelspalt. Im Applet gibt es
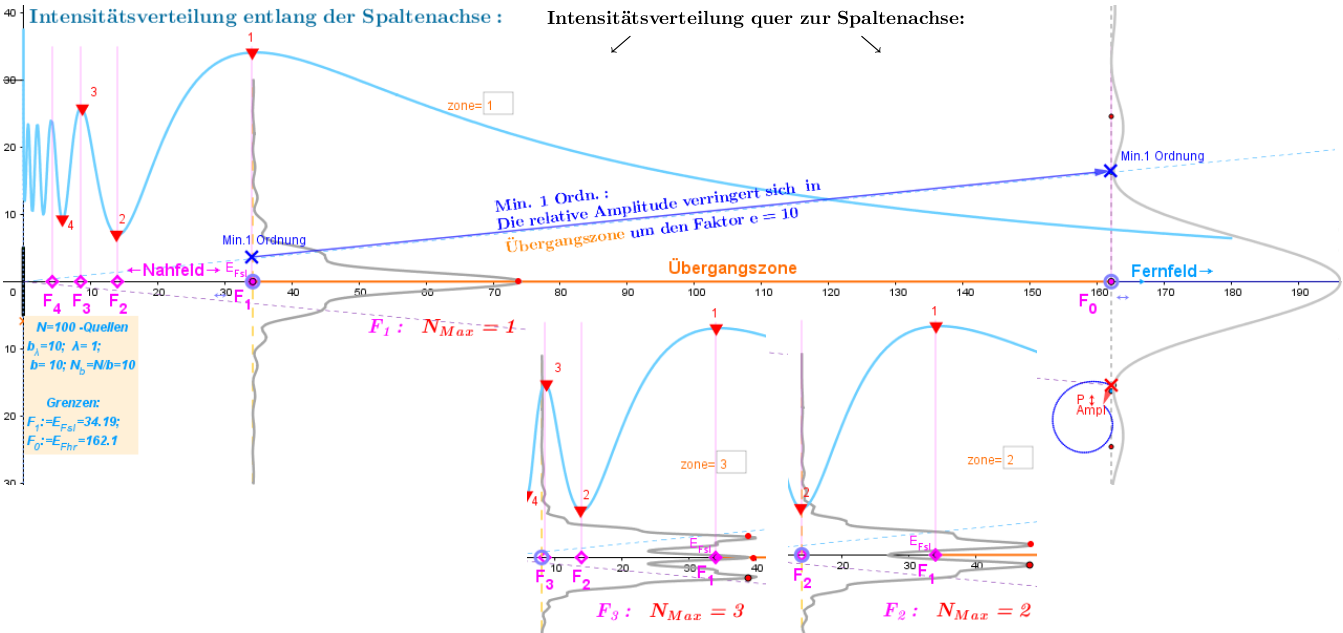
-zwei Verteilungenin Richtung der Längsachse des Spaltes: eine- für großen Abständen I=I(v) (Graphics 2), wo v:=b/ sqrt (2 λ x) -Fresnel-Parameter, andere- für geringen Abständen I=I(x) (Graphics) und
-Verteilung in Richtung der Querachse des Spaltes I=I(y) (Graphics).
# Stellen Sie sicher, dass diese Verteilungen nur von den Verhältniswerten bλ:=b/λ abhängen.
# Im Applet sind 100 Elementarstrahler als Vorgabe eingestellt. Probiere aus:
Was ändert sich, wenn Du die Zahl reduzierst? Jetzt erhöhe die Zahl: Ab welcher Zahl ergibt sich keine weitere wesentliche Änderungen mehr?
● Brennpunkte des Spaltes.
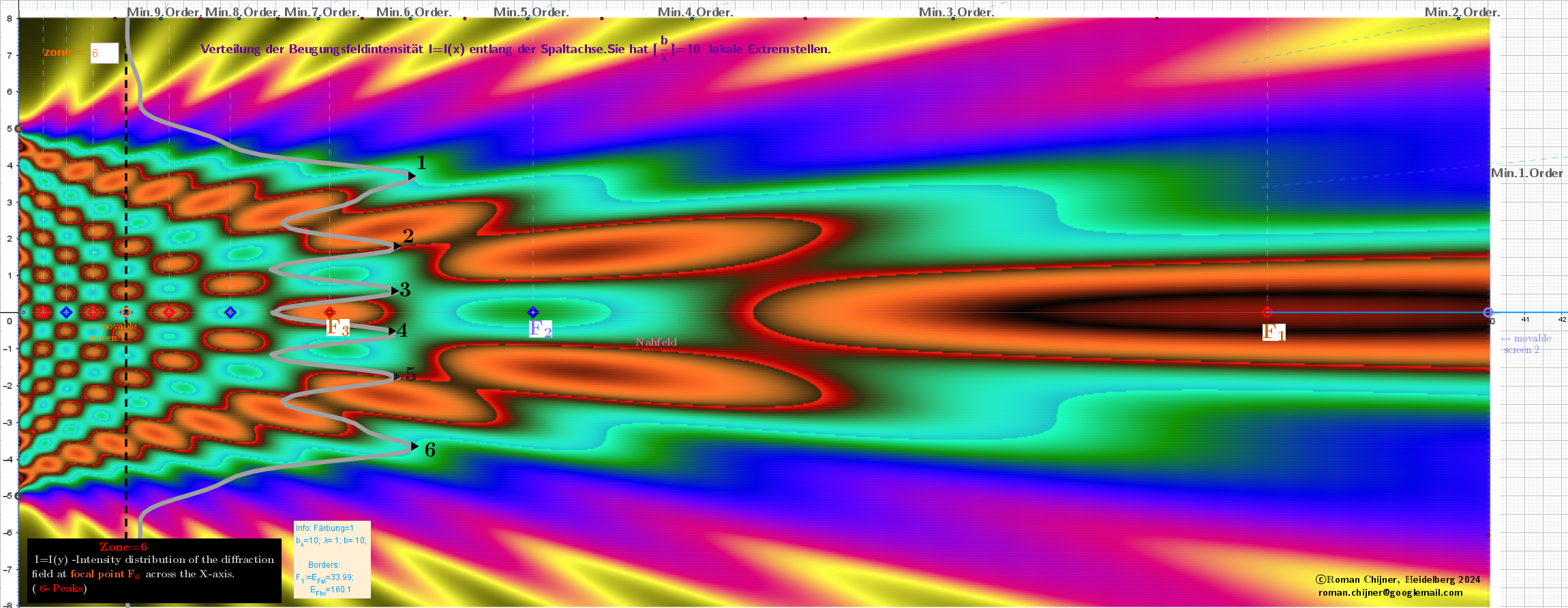
Die Abhängigkeit I= I (x) der Beugungsintensitätsverteilung hinter dem Spalt längs seiner Achse hängt nur von der relativen Größe ( bλ) des Spaltes ab. Die Positionen der Extrema dieser Abhängigkeit sind die Brennpunkte des Spaltes. Ihre Anzahl ist gleich ihrer relativen Größe bλ. Die Positionen der Extrema hängen von der Anzahl der Elementarstrahler ab. Um die Position von Brennpunkt F1 festzulegen, drücken Sie die max-Synchronisierungstaste (Grafik 2).
Die Positionen der Intensitätsextreme des Feldes auf der Spaltenachse der Fresnel-Kirchhoff'sche Beugungstheorie und Ergebnisse der numerischen Simulation zeigen hier eine gute Übereinstimmung.
● Wie definieren wir die Grenzen der Beugungsbereiche?
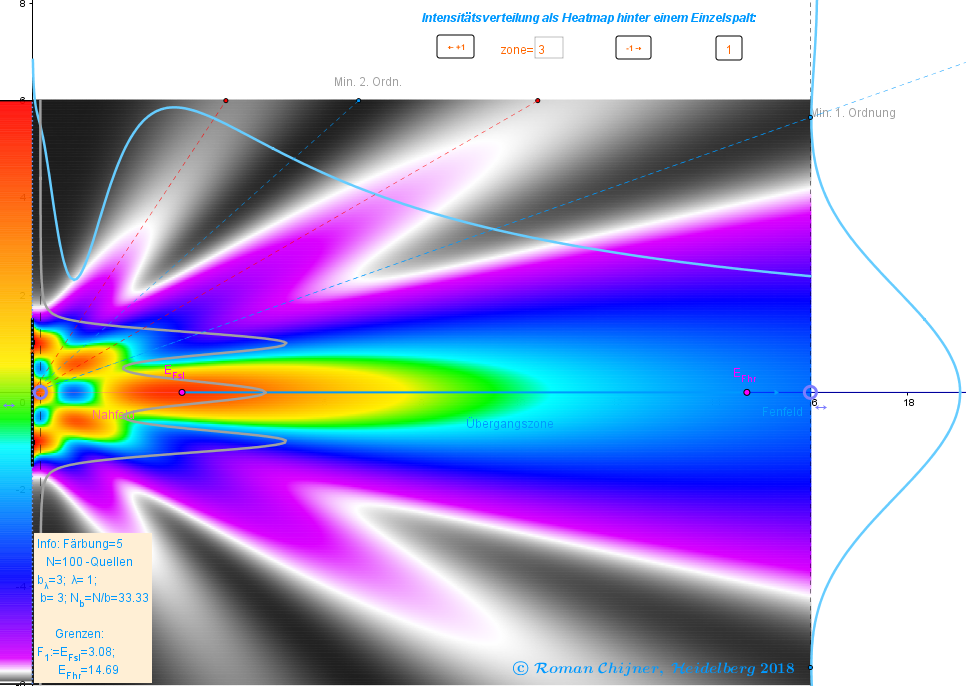
Nahfeldbereich ist Bereich der Fresnel-Approximation und Fernfeldbereich -Fraunhofer-Näherung: Interferenz in parallelen Strahlen.
Das letzte Maximum F1 (oder das erste Maximum der I= I (v) Verteilung) wird als Beginn des Übergangsbereichs angesehen. Betrachten wir die Strahlrichtung des ersten Beugungsminimums der Fraunhofer-Beugung: y= tan (φ) * x, wobei sin(φ) = λ / b. Dabei bleibt offensichtlich die Amplitude der Oszillation in dem Punkt dieses Strahls mit dem Spaltabstand F1 immer noch beträchtlich. Lassen Sie uns die Position des Punktes auf diesem Strahl finden, wo diese Amplitude, zum Beispiel, 10-mal schwächer wird. Der Spaltabstand dieses Punktes wird durch das F0- Ende der Übergangsregion und den Beginn der Fernfeldregion bezeichnet.
# Untersuchen Sie den Einfluss der Wellenlänge λ , Spaltenbreite b und der Anzahl der Strahler NQ auf die Beugungsgrenzen und die Positionen der Fraunhofer-Beugungsminima.
● Visualisierung des Lichtfeldes kann durch Abtasten im Abschnitt der Lichtfeldverteilung erfolgen. Um dies zu tun, müssen Sie „Scanpunkte“ mit der Schaltfläche "Execute"(taste klicken) erstellen und scanen.
Die Wellenlänge und die Spaltbreite können wir nach Wunsch auswählen. Bilder in: https://www.geogebra.org/m/aueuurys, https://www.geogebra.org/m/ztk9ssfj, https://www.geogebra.org/m/Q9zKrbnN
Darstellung des Beugungsphänomens hinter einem Spalt durch numerische Berechnung der Verteilung der Schwingungsintensität der überlappenden Elementarwellen.
Sei das optisches Spalt ist eine Menge der (n+1) Lichtpunktquellen von Elementarwellen. Nach dem Huygens-Fresnel`schen Prinzip gehen von jedem Punkt der Beugungsöffnung (eindimensionaler Spalt) Sekundärwellen aus, die hinter dem Spalt interferieren. Die Amplitude der resultierenden Lichtwelle im Punkt (xo,yo) ergibt sich durch die Addition der komplexen Einzelschwingungen:
A(xo,y0)=||
b/λ=3

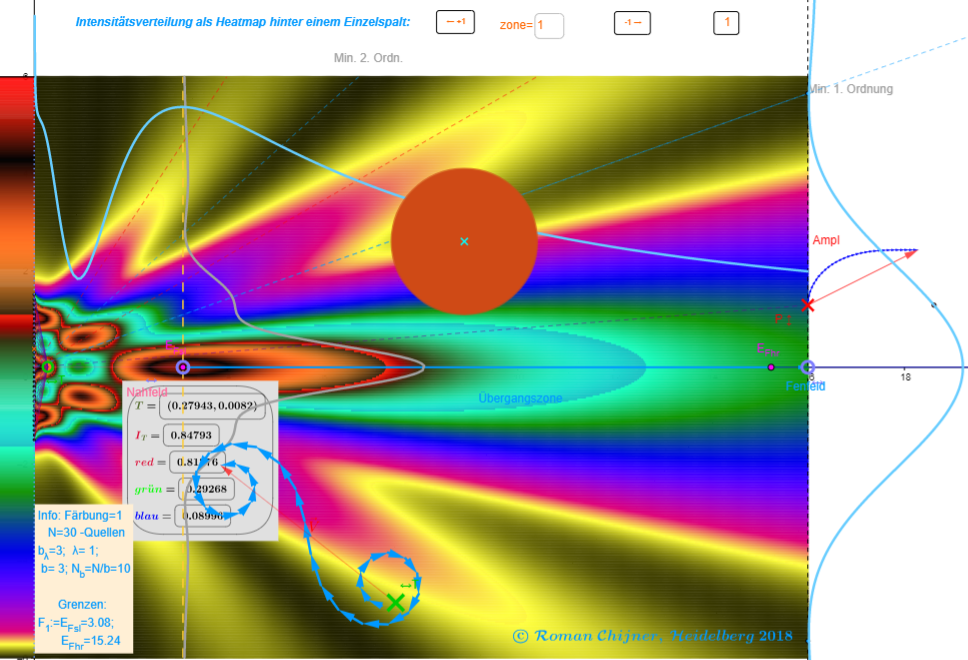

b/λ=10