Solving Equations (Lesson 6) OPTIONAL
Drills
The triangle and the square have equal perimeters. 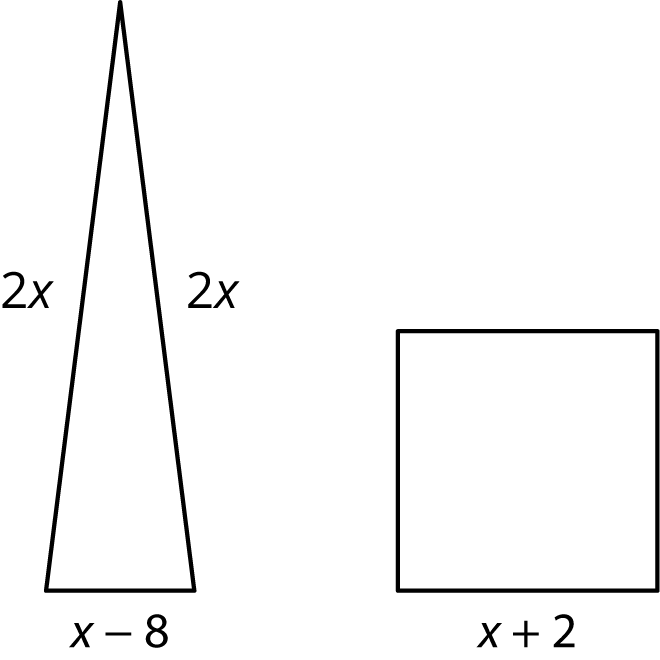
Ask groups to share their strategies for solving the question. Consider asking some of the following questions:
- “What expression represents the perimeter of the triangle? The perimeter of the square?” (The expression for perimeter of the triangle is 5x−8, and the perimeter of the square is 4(x+2).)
- “What was your strategy in making an equation?” (If both perimeters are the same, we can say their expressions are equal.)
- “What does x mean in the situation?” (It means an unknown value. None of the sides or perimeter is represented by x, so we cannot say it represents a specific thing on the figures.)
- “Looking at the figures, are there any values that x could not be? Explain your reasoning.” (Since the triangles have sides that are 2x, x cannot be 0 or a negative value. Triangles cannot have sides with 0 or negative side lengths. Since the third side is x−8, we can use this same reasoning to realize that x must actually be greater than 8.)
- “How does this information help when solving?” (If I make a mistake in my solution and get a value of x that is less than or equal to 8, then I know immediately that my answer is not reasonable and I can try to find my error.)
Without solving, identify whether these equations have a solution that is positive, negative, or zero.