Google Classroom
GeoGebraGeoGebra Classroom
GeoGebra

Lines and Angles (Module 4)

作者：Katia Clouse
主題：角度

G-CO.3.9

This activity gives students the opportunity to observe theorems [which] include: Vertical angles are congruent; when a transversal crosses parallel lines, alternate interior angles are congruent and corresponding angles are congruent; points on a perpendicular bisector of a line segment are [exactly those] equidistant from the segment’s endpoints.

REMEMBER:

Complementary angles are angles whose measures have a sum of 90 degrees. Supplementary angles are angles whose measures have a sum of 180 degrees.

DEFINITION

DEFINITION
A linear pair is defined as angles having a common side, and whose noncommon sides form opposite rays. In the diagram above, Angle 1 and Angle 2 form a linear pair. When angles share a common side, they are adjacent.

In this diagram, which ray is the common side for the adjacent angles and ?

勾選所有適當的選項
  • A
  • B
  • C
  • D
核對我的答案 (3)

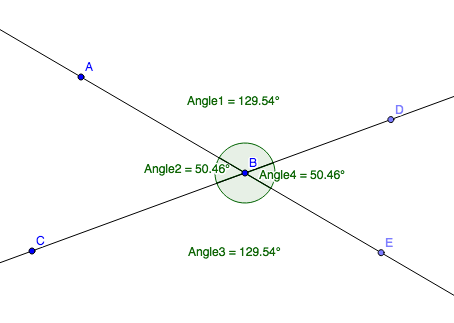
In the diagram below, click and drag points A and C to change the measures of the angles.

What do you notice is always true about the linear pair of angles?

勾選所有適當的選項
  • A
  • B
  • C
  • D
核對我的答案 (3)

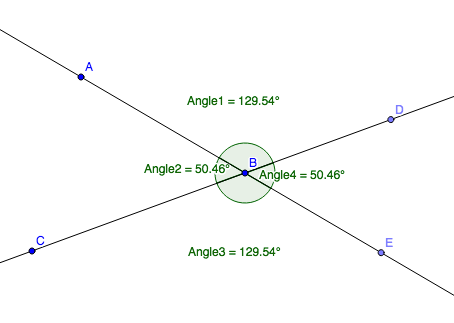
DEFINITION

DEFINITION
Vertical angles - nonadjacent angles formed by two intersecting lines. (Read: vertical angles do not have a common side)

In the diagram below, click and drag points A and C to change the measures of the angles.

What do you notice is always true about the vertical angles?

勾選所有適當的選項
  • A
  • B
  • C
  • D
核對我的答案 (3)

In the diagram above, which angles are vertical angles?

勾選所有適當的選項
  • A
  • B
  • C
  • D
核對我的答案 (3)

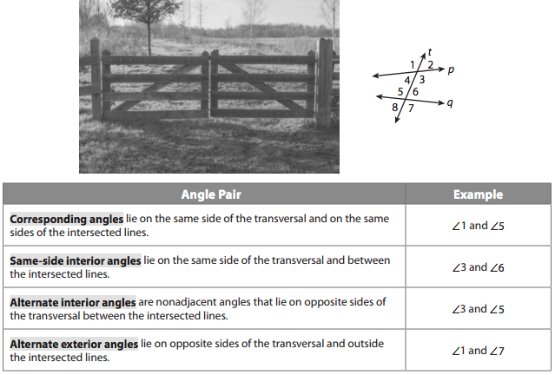
Note the kinds of angles formed by 2 lines p and q, and transversal t. This diagram is also in your text (p. 175).

Note the kinds of angles formed by 2 lines p and q, and transversal t. This diagram is also in your text (p. 175).
Here the two lines cut by a transversal are parallel. Click and drag point B to change the angle measures. Answer the questions below about what is ALWAYS true about these special angles when parallel lines are cut by a transversal.

Same-Side Interior Angles Postulate

If two parallel lines are cut by a transversal, then the same-side interior angles (like Angle Two and Angle Three) are

勾選所有適當的選項
  • A
  • B
  • C
核對我的答案 (3)

Corresponding Angles Theorem

If two parallel lines are cut by a transversal, then the corresponding angles (like Angle One and Angle Four) are

勾選所有適當的選項
  • A
  • B
  • C
核對我的答案 (3)

Alternate Interior Angles Theorem

If two parallel lines are cut by a transversal, then the alternate interior angles (like Angle One and Angle 3) are

勾選所有適當的選項
  • A
  • B
  • C
核對我的答案 (3)

What is line CD?

In the diagram below, which of the following provides the best description of line CD as it relates to segment AB?

勾選所有適當的選項
  • A
  • B
  • C
  • D
  • E
  • F
核對我的答案 (3)

Perpendicular Lines

Click and drag point D.

While the lengths are changing, is there anything that is always true?

勾選所有適當的選項
  • A
  • B
  • C
  • D
核對我的答案 (3)

最新資源

探索資源

探索主題