Puzzle: Divide triangle into 2 isosceles triangles ( integer lengths)
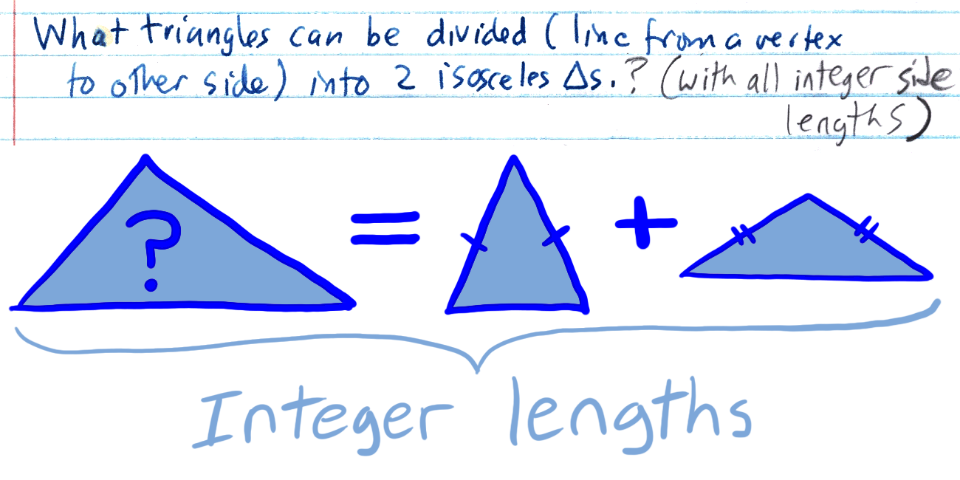
This diversion was passed along by my friend/colleague Andy Talmadge during a faculty meeting late in the 2023-24 academic year. To the best of his recollection, the question was inspired by something he had seen in some MAA magazine published a couple decades ago. The original puzzle may have asked for triangles that can be divided into two isosceles triangles with no restrictions on side length (i.e. either Andy added the requirement of integer side lengths, or I just assumed that's what he intended).
Within minutes I sensed that this puzzle could lead me down a deep, time-sucking rabbit hole.
It wasn't until a few months later in July when I finally prioritized a few days to fully indulge. Like so many satisfying problems, the premise of the question was simple, but a solution was elusive... and even once I found a solution, I still was left wondering:
- Was there an easier and/or more elegant approach?
- Is my set of solutions complete?
Solution (general)
This solution allows for the altitudes that divide each of the two isosceles triangle in half to have either irrational or integer lengths.
A more thorough writeup of the solution is here.
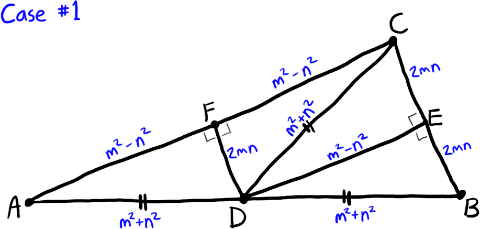
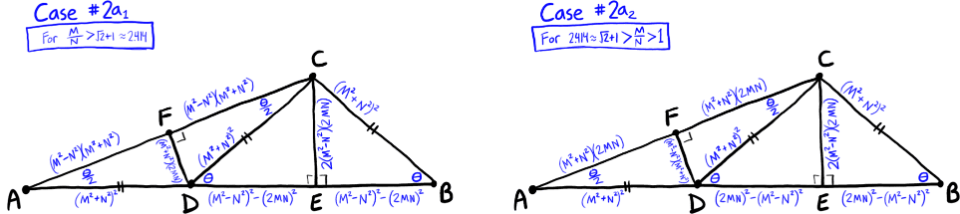
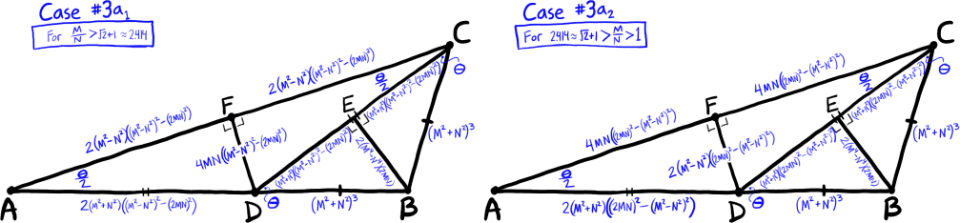
In brief, solutions are classified into three cases as shown in the figure.
To generate solutions with the GeoGebra construction below, first use the slider to select a Case.
Select a value for r by either typing an integer into the text box or using the ↑ or ↓ buttons.
Select a value for t by using the slider.
In most cases, the altitudes of the two isosceles triangles will be irrational.
Solution (original, with integer altitudes)
This was my first substantial attempt at a solution, prior to developing the superior solution above.
This solution requires that the altitudes that divide each of the two isosceles triangle in half have integer lengths.
The GeoGebra construction below churns out solutions. If inputs m and n for Case #1 (or M and N for Cases #2 & #3) meet the following conditions, it is believed that the solutions will be primitive and will not repeat solutions given by other m and n (or M and N) values.
- m>n>0 for integers m and n (or M>N>0 for integers M and N)
- m and n (or M and N) are relatively prime (have no common integer factors >1)
- m and n (or M and N) include one even value and one odd value
