Übung Pyramide
Übung zu Volumen und Mantelfläche der Pyramide
Das Quadrat ABCD mit a = 6 cm ist die Grundfläche der Pyramide ABCDS.
Der Punkt M ist der Diagonalenschnittpunkt der Grundfläche. ist die Höhe h der Pyramide.
Die Seitenflächen der Pyramide sind gleichseitige Dreiecke.
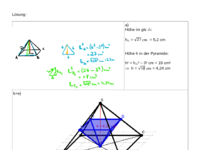
a) Berechne die Höhe h der Pyramide ABCDS. (Tipp: fertige zunächst eine Freihandskizze.)
b) Zeichne ein Schrägbild der Pyramide ABCDS mit AB als Schrägbildachse; q = 0,5; ω = 45°.
c) Berechne das Volumen der Pyramide ABCDS und den Inhalt ihrer Mantelfläche.
d) Sind die Dreiecke ABS und DBS kongruent zueinander? Untersuche die Dreiecke auf Gemeinsamkeiten.
e) Die Punkte E, F, G und H sind Mittelpunkte der Seitenkanten der Pyramide ABCDS, wobei . Zeichne die Pyramide EFGHM in das Schrägbild zu b) ein.
f) Berechne den prozentualen Anteil des Volumens der Pyramide EFGHM zum Volumen der Pyramide ABCDS.