Orthocenter - 2019
Constructing the Orthocenter
Steps to construct orthocenter.
Step 1: Use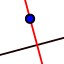 
to construct the line through A and perpendicular to BC.
Step 2: Use to construct the line through B and perpendicular to AC.
Step 3: Use to construct the line through C and perpendicular to AB.
Each line you constructed above contains an altitude of the triangle.
Step 4: Use 
to place a point where the altitudes intersect.
Step 5: Use 
to add a label to this point where the altitudes intersect.
to construct the line through A and perpendicular to BC.
Step 2: Use to construct the line through B and perpendicular to AC.
Step 3: Use to construct the line through C and perpendicular to AB.
Each line you constructed above contains an altitude of the triangle.
Step 4: Use to place a point where the altitudes intersect.
Step 5: Use to add a label to this point where the altitudes intersect.The point where all the altitudes intersect is called the orthocenter.
To answer the questions below, it might help to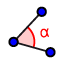 
measure each angle of the original triangle ABC.
measure each angle of the original triangle ABC.1. For what type of triangle is the orthocenter outside the triangle?
Select all that apply
- A
- B
- C
2. Move your triangle around so that the orthocenter is on a vertex. What is true about the triangle when this happens?
Select all that apply
- A
- B
- C
3. Move your triangle so that vertex A is directly above on a vertical line from the orthocenter. What is true about the triangle when this happens?
Select all that apply
- A
- B
- C