Discover Pythagorean Theorem
Learning Goal
Students will explore relationships between squares and right triangles, and learn the Pythagorean Theorem.
'Hypotenuse Squares'
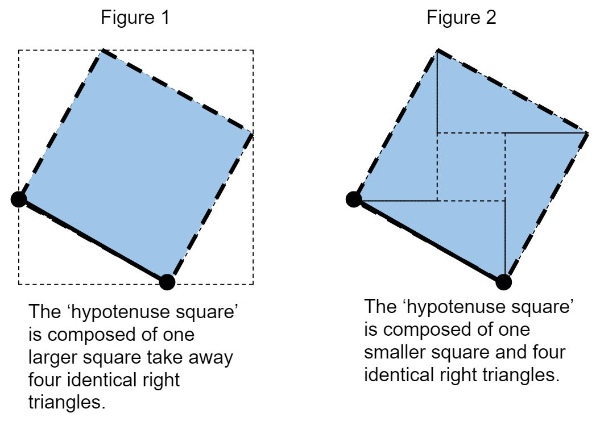
- Finding a composition of shapes to make the 'hypotenuse square'
- Finding the area of the square
- Finding the square root of the area
Visual 1: Click and drag the points to explore the distance between them.
Question 1: Use the Visual to...
Choose only ONE set of points, and use the 'hypotenuse square' to find the distance between them.
Hint: Review the 'Hypotenuse Squares' figures and explanation above.
Question 1: Check your answer.
What's next?
Finding the distance between two points (or the length of the hypotenuse) is possible by finding the square root area of the 'hypotenuse square'. Now, we will look for a simpler way to find the area of this square.
Visual 2: Click and drag the points to explore the patterns between the side lengths of a right triangle.
Question 2: Use the Visual to...
List the 3 square areas for a right triangle with each set of side lengths.
What patterns do you see within each list of areas?
Bonus: Use the words leg and hypotenuse.
Question 2: Check your answer.
Visual 3: Click and drag the circles to move the area pieces.
Question 3: Use the Visual to...
Describe what is happening in your own words.
Question 3: Check your answer.
What's next?
Finding the distance between two points (or the length of the hypotenuse) becomes more straightforward if we use the relationship between the squares of the sides of a right triangle.
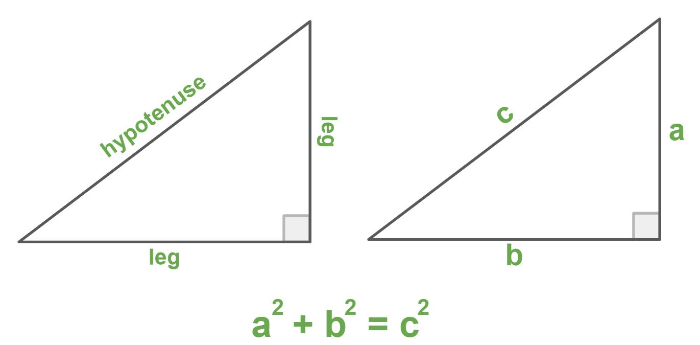
This relationship is called The Pythagorean Theorem and is often represented by this equation: , where and are the lengths of the legs (shorter sides) and is the length hypotenuse (longer side).
The Pythagorean Theorem
Visual 4: Click and drag the points to explore the distance between them.
Question 4: Use the Visual to...
Find the hypotenuse 'c' for each set of leg lengths ('a' & 'b').
Hint: Use the Pythagorean Theorem, .