Haces superpuestos: Cálculo de un rayo doble conocido el otro
Figura de Análisis
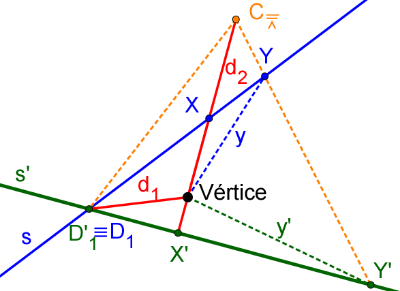
Problema dual a este.
Este problema puede resolverse de dos maneras, pero ambas emplean la misma figura de análisis.
Si consideramos dos series perspectivas, con base las rectas s y s', parejas de puntos homólogos están alineados con el centro perspectivo. Si se proyectan ambas series desde un Vértice se obtienen dos haces superpuestos. En estos haces superpuestos aparecen dos rayos dobles. El primero es el rayo proyección del punto de corte de las bases D1=D'1. El segundo, el rayo que contiene al centro perspectivo.
La metodología de resolución consiste en aplicar la figura de análisis al problema presente. Existen dos construcciones distintas. Tenemos uno de los rayos dobles, d'1=d1. La primera construcción (deslizador "Construcción=1") es considerar dos series perspectivas (de bases s y s') cuyo punto de corte pertenece al rayo doble. Si determinamos el centro perspectivo de esas dos series, el rayo desde V que pasa por él es el otro rayo doble (mover el deslizador "Paso" para ver los distintos pasos de la construcción).
La otra opción (deslizador "Construcción=2") es colocar un centro perspectivo en el rayo doble conocido. Si se secciona uno de los haces con una recta r cualquiera, queda definida inmediatamente (con el centro perspectivo) la recta r', y por lo tanto el punto de corte de r y r', por donde pasa el rayo solución.
Nótese que las rectas del enunciado se pueden mover con los puntos (rombos) grises.