Definizioni e assioma della parallela
Rette parallele
Due rette si dicono parallele se non hanno punti in comune oppure se coincidono.
Si considerano parallele anche due rette coincidenti per avere la proprietà riflessiva e far in modo che il parallelismo sia una relazione d'equivalenza.
Striscia
Date due rette parallele distinte r ed s, si chiama striscia di lati r ed s l'intersezione dei due semipiani individuati da una delle due rette r ed s che contengono l'altra retta, cioè l'intersezione tra il semipiano che ha come origine r e contiene s e il semipiano che ha come origine s e contiene r.
Abbiamo visto che dati un punto P e una retta r, esiste sempre una e una sola retta passante per P che sia perpendicolare ad r.
Possiamo affermare la stessa cosa per la retta parallela?
Dati un punto P e una retta r, esiste sempre una e una sola retta passante per P che sia parallela ad r?
La risposta non è tanto semplice.
Si può dimostrare che dati un punto P e una retta r, esiste una retta passante per P che sia parallela ad r.
Ma non si può dimostrare che la parallela è unica!
L'unicità della parallela a una retta, passante per un punto, non si può dimostrare a partire dagli assiomi che abbiamo assunto e dai teoremi che abbiamo dimostrato.
Costruzione della retta parallela a una retta data r, passante per un punto P
- Se il punto P appartiene alla retta r, la retta parallela ad r e passante per P è la retta stessa r.
- Se il punto P non appartiene alla retta r, conduciamo da P la retta perpendicolare ad r (che esiste per il teorema della perpendicolare) e la chiamiamo n (normale). Per il punto P consideriamo anche la retta perpendicolare ad n (che esiste per il teorema della perpendicolare) e la chiamiamo s. Dimostriamo che questa retta s perpendicolare ad n è parallela ad r.
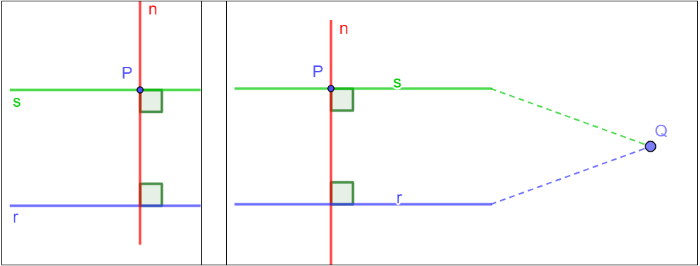
Teorema: rette perpendicolari alla stessa retta
Due rette perpendicolari alla stessa retta sono parallele.
Ipotesi: r n, s n
Tesi: r s
Dimostrazione per assurdo
Supponiamo che r ed s non siano parallele. Allora, deve esistere un punto Q in cui r ed s si incontrano.
Ma in questo caso, per il punto Q passano due rette, r ed s, perpendicolari ad n.
E questo è assurdo per l'unicità della perpendicolare.
Le Geometrie non euclidee
Per anni i matematici hanno cercato di dimostrare che il Quinto postulato di Euclide (o assioma della parallela) non fosse necessario, che fosse possibile dimostrarlo a partire dagli altri assiomi o dai teoremi, ma alla fine si sono convinti dell'impossibiltà di dimostrare il quinto postulato. Non si può dimostrare, non deriva dagli altri assiomi. Eliminandolo dalla lista degli assiomi si costruiscono le geometrie non euclidee.
Nelle geometrie non euclidee non è vero che dati un punto P e una retta r, esiste sempre una e una sola retta passante per P che sia parallela ad r.
Le Geometrie non Euclidee nascono dalla negazione del quinto postulato e di tutti i teoremi che si dimostrano applicando il quinto postulato.
L'enunciato del quinto postulato (nella formulazione di Playfair -1795) è:
Data una retta ed un punto non appartenente ad essa, esiste ed è unica una retta passante per il punto e parallela alla retta data.
La negazione di questa proposizione equivale a negare le sue due affermazioni, quella dell'esistenza e quella dell'unicità. Quindi, si hanno due possibili negazioni:
- Data una retta ed un punto non appartenente ad essa, esistono infinite rette passanti per il punto e parallele alla retta data.
- Data una retta ed un punto non appartenente ad essa, non esiste una retta passante per il punto e parallela alla retta data.
Assioma della parallela (formulazione del libro)
Dati un punto P e una retta r, la retta passante per P e parallela ad r è unica.