Vijf gevallen mogelijk
Een regelmatig veelvlak is alleen mogelijk indien de hoekensom van de regelmatige veelhoeken die in één punt samenkomen kleiner is dan 360°
Er geldt dan voor een stel getallen n en m dat deze hoekensom gelijk is aan:
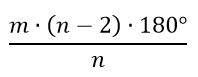
Deze hoekensom moet kleiner zijn dan 360° !
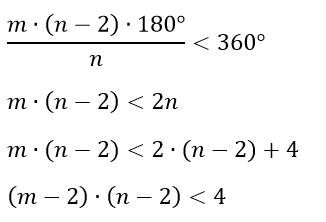
Wij gaan dus op zoek naar twee getallen n en m waarvoor het product van de factoren (m-2) met (n-2) kleiner is dan 4.
De eerste factor (m-2) MOET dus kleiner dan of gelijk aan 3 zijn.
Idem voor de factor (n-2)
Wij overlopen systematisch de mogelijkheden:
(m - 2) = 3 met (n - 2 ) = 1
m = 5 met n = 3
Een twintigvlak.
(m - 2) = 2 met (n - 2 ) = 1
m = 4 met n = 3
Een achtvlak.
(m - 2) = 1 met (n - 2 ) = 1
m = 3 met n = 3
Een viervlak.
(m - 2) = 1 met (n - 2 ) = 2
m = 3 met n = 4
Een zesvlak (kubus).
(m - 2) = 1 met (n - 2 ) = 3
m = 3 met n = 5
Een twaalfvlak.
