하가의 정리 1
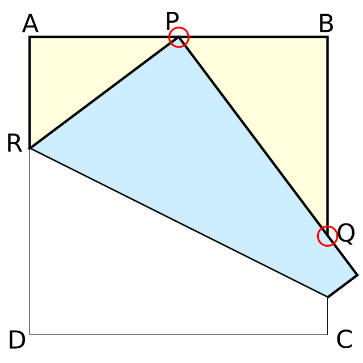
하가의 정리란?
정사각형의 한 변은 항상 임의의 유리수 비로 분할 될 수 있습니다. 하가의 정리는 이러한 분할을 사용하여 특별한 유리수의 길이를 갖는 작도를 할 수 있음을 보여줍니다.
하가의 정리와 같이 접는 다면 아래 표와 같은 관계가 항상 성립합니다.
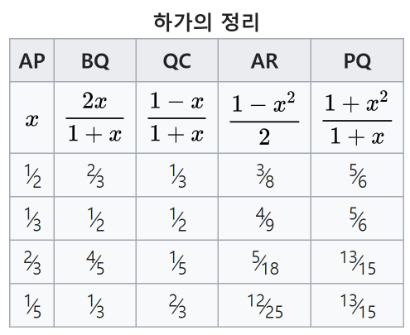
이때, (인 자연수)로 놓으면 그 길이는 아래와 같이 바뀐다.
따라서 의 값을 잘 고르면 하가의 정리를 이용해서 원하는 꼴의 유리수 길이를 빠르게 접을 수 있음을 알 수 있다.
이번엔 나머지 변도 을 이용해서 나타내어 보자. 이므로 이를 일반화한 결과에 대입하면 나머지 변의 길이도 구할 수 있다.
△EAP에서 세 변의 길이 는 각각 이다.
이때 세 변의 길이를 으로 통분한 뒤 길이비를 구하면
이 된다.
은 인 자연수이므로 의 길이비도
도 자연수가 됨을 알 수 있다. 즉, △EAP는 길이비가 항상 피타고라스 세 쌍이 되는 직각삼각형이다.
재미있는 것은 피타고라스 세 쌍을 만드는 방법과 △EAP는 길이비의 관련이 있다는 점이다.
[피타고라스 세 쌍]
피타고라스 세 쌍은 직각삼각형에 대한 피타고라스의 정리 을 만족하는 세 쌍의 자연수를 말한다. 특히, 피타고라스 세 쌍 중 서로소인 세 정수로 피타고라스 세 쌍을 원시 피타고라스 세 쌍(primitive Pythagorean triple)이라고 부른다. 모든 피타고라스 세 쌍은 원시 피타고라스 세 쌍의 배수라고도 할 수 있다.
아래 공식은 피타고라스 세 쌍을 만드는 유클리드 공식이다.
, , (인 자연수)
따라서, 하가의 정리는 모든 피타고라스 세 쌍을 만드는 것이 가능하다고 결론 내릴 수 있다.
참고 자료 :
1. 피타고라스 삼조 - 위키백과, 우리 모두의 백과사전 (wikipedia.org)
2. 피타고라스 쌍(Pythagorean triple) - 수학노트 (mathnt.net)
3. Pythagorean triple - Wikipedia
4. Diophantine equation - Wikipedia