Teorema sobre segmentos paralelos en un triángulo
Cambia la forma del triángulo, moviendo los vértices; luego mueve el punto D y observa la relación entre los segmentos.
En el ∆ABC, si DE‖BC entonces se cumple que:
AD/AB = AE/AC y AD/DB = AE/EC
Ejercicio 1
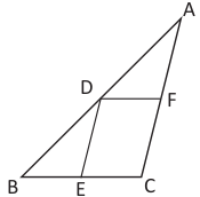
¿Qué triángulos de los que se forman son semejantes entre sí?
¿Cuáles segmentos son proporcionales?
Ejercicio 2
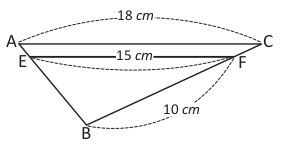
En el ABC, EFAC, ¿cuál es la longitud del lado BC? Escribe solo el número, sin unidad de medida.
Ejercicio 3
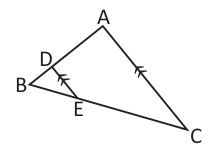
Calcula la longitud de EC en el triángulo ABC, si BD = 4 cm, DA = 10 cm y BE = 6 cm
Ejercicio 4
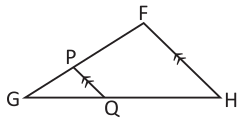
En el FGH, PQ ‖ FH. Calcula la longitud del lado FG, si PG = 6 cm, GQ = 8 cm y QH = 12 cm