Teorema: Circonferenza passante per tre punti
Esiste una e una sola circonferenza passante per tre punti non allineati.
Ipotesi: A, B e C sono tre punti non allineati
Tesi: Esiste una sola circonferenza passante per A, B e C
Si tratta di una dimostrazione costruttiva; cioè, per dimostrare l'esistenza di una tale circonferenza la costruiamo, forniamo un procedimento per costruirla.
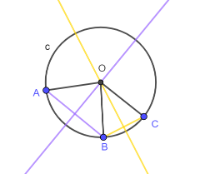
Dimostrazione: Esistenza
Consideriamo l'asse del segmento AB e l'asse del segmento BC.
Dato che i tre punti non sono allineati, i due assi dei segmenti non sono paralleli e quindi, si incontrano in un punto O.
OA OB perchè O appartiene all'asse di AB e quindi, deve essere equidistante dai suoi estremi;
OB OC perchè O appartiene all'asse di BC e quindi, deve essere equidistante dai suoi estremi.
Pertanto, OA OB OC per la proprietà transitiva; cioè, O è equidistante da A, B e C.
Prendendo la circonferenza di centro O e raggio OA, abbiamo una circonferenza che non solo passa per A, ma anche per B e C. Abbiamo costruito la circonferenza passante per i tre punti.
Dimostrazione: Unicità
La circonferenza che abbiamo costruito è unica perchè è unico il punto da prendere come centro, l'intersezione degli assi dei due segmenti AB e AC.
Costruzione della crf passante per A, B e C non allineati
Non esistenza della circonferenza passante per tre punti allineati
Non può esistere una circonferenza passante per tre punti allineati A, B e C perchè non esiste il centro, che dovrebbe essere l'intersezione degli assi dei segmenti AB e BC.
Dato che i punti A, B e C sono allineati, gli assi di AB e BC sono paralleli e quindi, non intersecandosi, non individuano un punto che possa essere il centro della circonferenza.