Demostración de la conjetura
En primer lugar, consideraremos una triangulación de la sala que no necesite agregar otros vértices. Siguiendo la estrategia anterior, trataremos de probar que toda triangulación es 3-coloreable, mediante el principio del efecto dominó.
i) La primera ficha de nuestro dominó será la sala más simple. Es decir, una triangular de n=3 lados. Esta ficha cae, es decir, esta sala es 3-coloreable.
ii) Consideramos una ficha distinta de la primera, es decir, una sala cualquiera con un número de lados n>3 y suponemos que todos los polígonos con menos lados que n pueden ser 3-coloreable. Entonces, se podría preguntar a los alumnos si también caerá esta ficha.
Dada una triangulación de esta sala de n lados, con n>3, vamos a dividirla en dos mitades. Para ello, escogemos dos vértices cualesquiera que estén conectados mediante una diagonal. En la Figura 6, hemos escogido la diagonal AC, que separa en dos la triangulación total del polígono de n lados ABCD···. Por un lado, tenemos el triángulo ABC, y por otro, la triangulación del polígono ACD···. Estas dos triangulaciones pertenecen a polígonos cuyo número de lados es menor que 
. Como habíamos supuesto que todas las salas con menos de n lados son 3-coloreable, entonces la triangulación ACD··· también será 3-coloreable, debido a la suposición (ii) anterior.
Figura 6
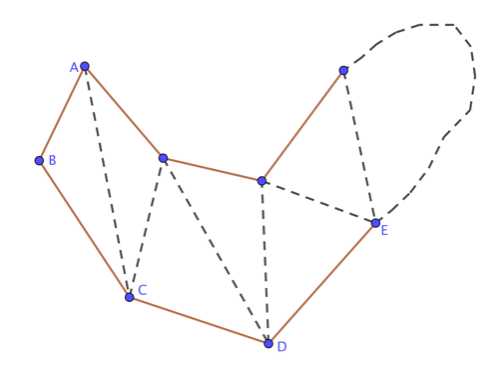
Para acabar de ver que toda la triangulación ABCD··· es 3-coloreable, solo faltará colorear el vértice 
de un color distinto al que tengan A y C en la triangulación ACD··· (Figura 6). Así pues, toda triangulación de una sala cualquiera dada es 3-coloreable.
Por último, como hay n vértices, existe al menos un color que se utiliza como mucho para [n/3] vértices. Ahora bien, este color estará presente en todos los triángulos de la triangulación; si colocamos una cámara en cada uno de esos vértices tendremos asegurada la vigilancia de la totalidad de la sala poligonal, tal y como queríamos demostrar.