"Loxodrome" ? Oder nicht ?
Übrigens: dieses Büchlein ist in der geogebra-Suche unter Loxodrome nicht zu finden! Wahrscheinlich stören die " - "?!
Dieses kleine GeoGebra-Buch mit 14 Seiten stellt die Frage:
Wie soll man die Kurven nennen, die aus Loxodromen durch Spiegelung an einem Kreis
- oder allgemeiner - unter einer Möbiustransformation entstehen?
Nach wikipedia ist ...
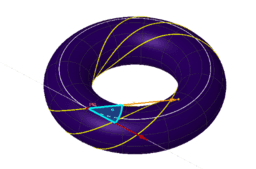
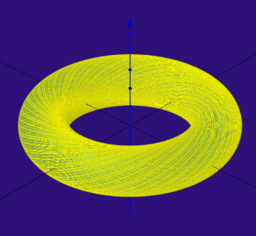
- Eine Loxodrome (gr. loxos „schief“, dromos „Lauf“) ist eine Kurve auf einer Kugeloberfläche – z. B. der Erdoberfläche –,
die die Meridiane im geographischen Koordinatensystem immer unter dem gleichen Winkel schneidet und daher auch
Kursgleiche, Winkelgleiche oder Kurve konstanten Kurses genannt wird.
Auf der Erde sind diese Kurven ausgezeichnet wegen der besonderen Lage von Nord- und Südpol als Folge des Magnetfeldes.
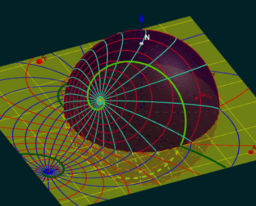
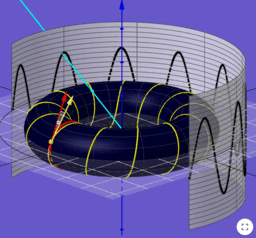
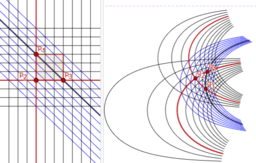
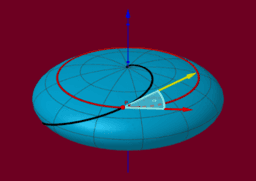
Loxodrome schneiden "Meridiane" (Längskreise) bzw. die Breitenkreise jeweils unter konstantem Winkel.
Betrachtet man die Erde nur als Kugel, so könnte man 2 beliebige, diametral liegende Punkte als Nord- und Südpol bezeichnen. Die hierzu gehörenden "Loxodrome" entstehen aus den herkömmlichen Loxodromen einfach durch eine Drehung der Kugel um den Mittelpunkt.
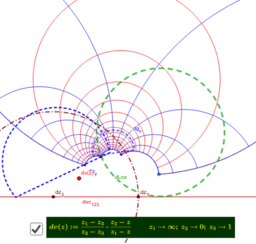
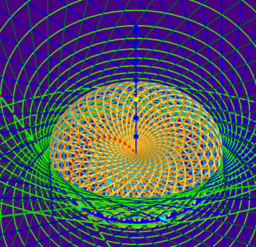
Mehr noch: geogebra erlaubt es, mit einem einzigen Klick in die Welt der Möbiusgeometrie einzutauchen: Gespiegelt an irgendeinem Kreis werden aus Längs- bzw. Breitenkreisen die Kreise von hyperbolischen bzw. elliptischen Kreisbüscheln. Die Bilder der Loxodromen werden Kurven, welche diese Kreise "winkelgleich" schneiden!
Wie soll man diese Kurven nennen? Als Möbiusgeometer würden wir diese Kurven gerne ebenfalls als Loxodrome bezeichnen!