Geradlinige Bewegung

Autor:
Gottfried Kendl
Thema:
Vektoren 2D (zweidimensional), Geometrie, Geraden, Vektoren

Beispiel

Ein Käfer befindet sich zum Zeitpunkt t = 0 im Punkt P. Er bewegt sich auf einer Geraden mit konstanter Geschwindigkeit, der Geschwindigkeitsvektor sei (in Längeneinheiten pro Sekunde).
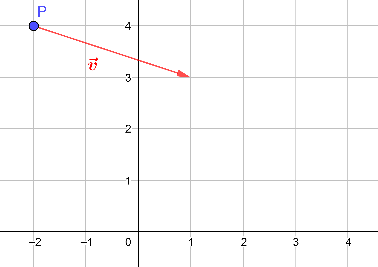
Image

Aufgabe A

Übertrage die obige Abbildung ins Heft und gib die Koordinaten von P und an. An welchem Ort X befindet sich der Käfer nach 1 s, 2 s, 3 s, s, vor 1 s? Gib zu jedem t-Wert die Koordinaten von X an. (Fülle die Tabelle im Heft aus.) 

t 0 1 2 3  -1
X

Antwort überprüfen

Aufgabe B

Wie kann man X mit Hilfe von P und berechnen? Gib zu jedem t-Wert den passenden Term an. (Fülle die Tabelle im Heft aus.)

t 0 1 2 3   -1
X PP +

Antwort überprüfen

Bewege X, indem du t änderst.

Man erkennt:

  • Jedem Wert von t entspricht genau ein Punkt X der Geraden.
  • Jedem Punkt X der Geraden entspricht genau ein Wert von t.
     Die Formel beschreibt also - auch unabhängig von einer Bewegung - die Gerade, die durch den Punkt P und den Vektor festgelegt ist. Man nennt die Formel eine Parameterdarstellung der Geraden. nennt man einen Richtungsvektor der Geraden, t heißt Parameter. Richtungsvektoren werden oft mit dem gleichen Buchstaben wie die Gerade bezeichnet, also z.B.   g: X = P + t   h: X = Q + t

Aufgabe C

Gib eine Parameterdarstellung der oben dargestellten Geraden (mit konkreten Zahlen) an.

Antwort überprüfen

Neue Materialien

Entdecke Materialien

Entdecke weitere Themen