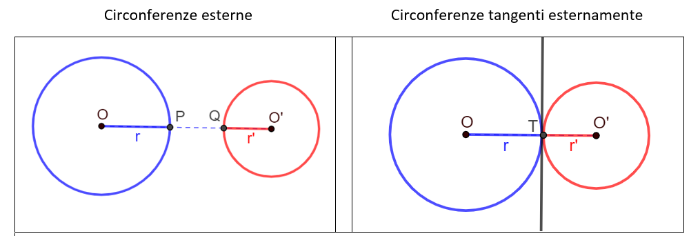
Teorema
Posizione reciproca di due circonferenze
Consideriamo due circonferenze di raggi r e r', con r r', e centri O e O'.
- Le due circonferenze sono esterne se e solo se la distanza tra i centri è maggiore della somma dei due raggi: OO' > r + r'
- Le due circonferenze sono tangenti esternamente se e solo se la distanza tra i centri è congruente alla somma dei due raggi: OO' = r + r'
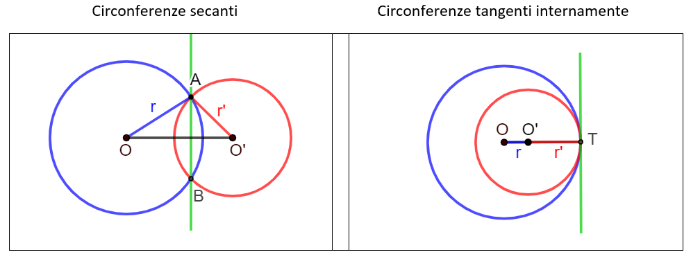
Posizione reciproca di due circonferenze
Consideriamo due circonferenze di raggi r e r', con r r', e centri O e O'.
- Le due circonferenze sono secanti se e solo se la distanza tra i centri è minore della somma dei due raggi e maggiore della loro differenza: r - r' < OO' < r + r' (disuguaglianza triangolare applicata al triangolo AOO')
- Le due circonferenze sono tangenti internamente se e solo se r > r' e la distanza tra i centri è congruente alla differenza dei due raggi: OO' r - r'
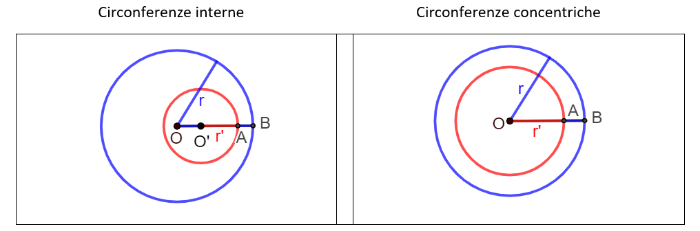
Posizione reciproca di due circonferenze
Consideriamo due circonferenze di raggi r e r', con r r', e centri O e O'.
- Le due circonferenze sono interne (o una interna all'altra) se e solo se r > r' e la distanza tra i centri è minore della differenza tra i due raggi: OO' < r - r' (disuguaglianza triangolare applicata al triangolo AOO')
- Le due circonferenze sono concentriche se e solo se r > r' e la distanza tra i centri è nulla, cioè i centri sono coincidenti: OO' = 0