Transformatie van drie punten op een lijn
De opdracht is om drie punten op een lijn projectief af te beelden zodat
de punten A, B en C projectief zijn met B, C en A.
Punt  en llijn zijn willekeurig en dat geeft de punten
en llijn zijn willekeurig en dat geeft de punten  ,
,  en
en 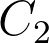 .
Op
.
Op  kies je willekeurig (niet op die andere punten natuurlijk)
kies je willekeurig (niet op die andere punten natuurlijk)  en
en 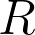 .
Dan zijn de punten
.
Dan zijn de punten 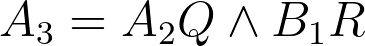 en
en  .
Projectie vanuit
.
Projectie vanuit  geeft
geeft 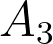 ,
, 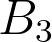 en
en  .
En projectie vanuit
.
En projectie vanuit 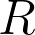 geeft
geeft  ,
,  en
en 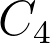 .
En daarmee zijn de punten
.
En daarmee zijn de punten 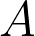 ,
, 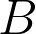 en
en  cyclisch verwisseld.
cyclisch verwisseld.
Uitgangspunt zijn de drie punten A_1, B_1 en C_1. Deze worden perspectief afgebeeld vanuit punt P op de reeks A_2, B_2 en C_2. Op de lijn C_2A_1 worden twee perspectiviteitscentra Q en R gekozen. Vanuit Q worden de punten A_2, B_2 en C_2 perspectief afgebeeld op de punten A_3, B_3 en C_3. Voorts worden deze punten vanuit het punt R afgebeeld op A_4, B_4 en C_4. Deze laatste benaming is een hernoeming van de oorspronkelijke punten B_1, C_1 respectievelijk A_1.