쪽매맞춤이란?
합동인 도형을 이용하여 평면을 빈틈없이 겹치지 않고 덮는 것을 쪽매맞춤(Tessellation, 테셀레이션)이라고 한다. 쪽매맞춤의 대중화에 기여한 사람은 네덜란드의 화가 M.C.에셔이다. 1963년 여름 알함브라 궁전을 방문하고 난 후 에셔는 자신의 예술적 관심을 완전히 바꾸게 된다. 그는 14세기 궁전의 벽을 장식하고 있는 기하적 무늬들에 깊은 충격을 받았고, 꼬박 3일을 그 곳에서 보내며 기하적 주제들을 연구하였다. 기하적 원리와 수학적개념을 토대로 무한, 상대성, 반사, 반전, 그리고 닮음을 작품에 반영하였고, 창조적 형태의 작품 세계를 구축하였다.
[과제1~2] 다음 작품은 쪽매맞춤을 이용한 에셔의 두 작품과 프랑스의 작가 알랭 니콜라스의 작품이다. 각 물음에 답하시오.
(가)
(나)
(다)
위의 (가), (나), (다) 작품에 이름을 붙여보시오.
작품에서 반복되는 모양은 무엇이고, 어떤 방식으로 반복되고 있는지 말하시오. 예를 들어 무늬의 배열 방법이나 무늬를 만드는 방법 등을 적어보시오.
우리 주변에서 모양이 맞물려서 면을 빈틈없이 덮는 것을 본 적이 있는지 생각해보고, 그 예를 찾아보시오. (사례를 설명하거나, 웹에서 관련된 이미지를 찾아 이미지의 주소를 작성하세요.)
정다각형은 모든 각의 크기가 서로 같으며 모든 변의 길이도 서로 같은 다각형이다.
정다각형을 이용한 쪽매맞춤의 종류에는 한 가지 정다각형만을 이용한 정규 쪽매맞춤과 두 가지 이상의 정다각형을 이용하는 준정규 쪽매맞춤이 있다.
[과제4~6] 다음 활동을 통해 정규 쪽매맞춤에 대해 탐구하시오.
아래 프로그램 사용법을 참고하여 정규 쪽매맞춤이 가능한 정다각형들을 탐구하시오.
※ 프로그램 사용법
- 그리고자 하는 정다각형 도구를 선택하고 두 점을 찍으면 두 점을 잇는 선분을 한 변으로 하는 정다각형이 그려진다.
- 두 점을 찍는 순서에 따라 나타나는 방향이 달라지므로 순서에 유의하시오.
- 이동 도구
를 이용하여 도형이나 화면을 이동시킬 수 있다. - 마우스 휠 버튼을 이용하거나
, 
도구를 이용하여 화면을 확대, 축소할 수 있다. - 쪽매맞춤이 가능한 정다각형의 조합을 찾기 위해 하나의 정다각형을 그리고, 그 정다각형의 점을 이용하여 새로운 정다각형을 만들어갈 수 있다.
다음 다각형 중에서 정규 쪽매맞춤에 사용할 수 있는 정다각형은 무엇인가?
정삼각형, 정사각형, 정오각형, 정육각형, 정칠각형, 정팔각형, 정구각형, 정십각형
정규 쪽매맞춤이 가능한 경우 각 꼭짓점에 몇 개의 정다각형이 모이게 되는지 관찰하고 그 결과를 정리하시오.
[과제7~8] 그림과 같이 두 가지 이상의 정다각형을 이용한 쪽매맞춤을 준정규 쪽매맞춤이라고 한다. 아래의 애플릿을 이용하여 준정규 쪽매맞춤을 만들어보시오.
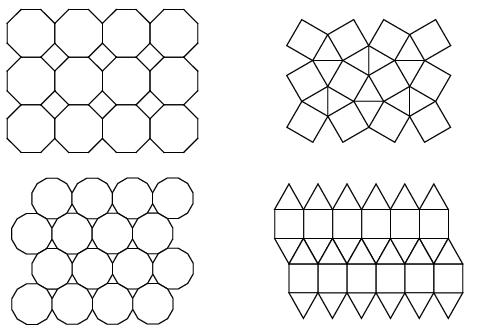
다음과 같은 환경에서 준정규 쪽매맞춤을 만들어보시오.
준정규 쪽매맞춤이 가능한 정다각형을 찾는 순서나 전략에 대해 생각해보고 그 결과를 작성해보시오.