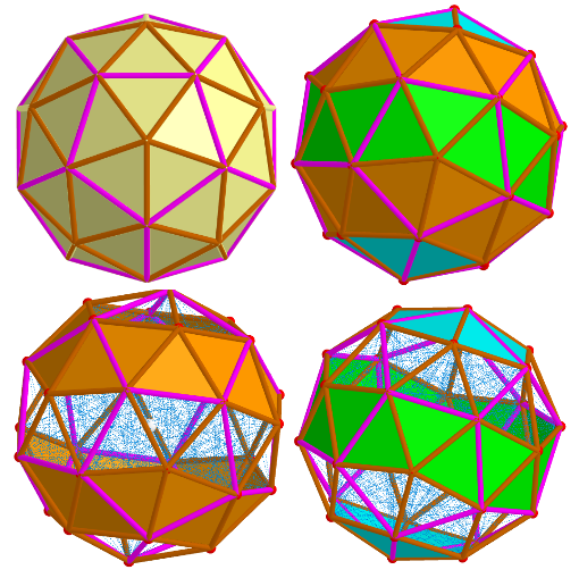
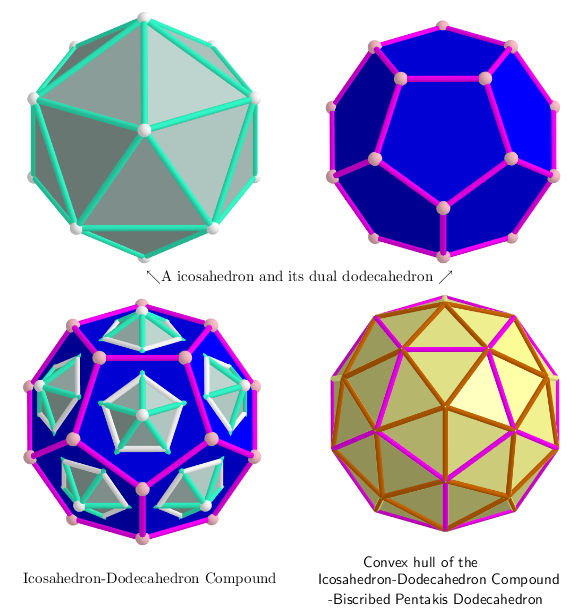
Biscribed Pentakis Dodecahedron: The Icosahedron-Dodecahedron Compound whose all vertices lie on the same sphere
Biscribed Pentakis Dodecahedron
Vertices: 32 (12[5] + 20[6]); Faces: 60 (isosceles triangles); Edges: 90 (60 short + 30 long)
Symmetry: Full Icosahedral (Ih)
Short Edge Angle: acos(−(255*sqrt(5)−7
+sqrt(6*(5105+2099*sqrt(5))))/898) ≈153.789590509 degrees
Long Edge Angle: acos(−(560−195*sqrt(5)
+12*sqrt(15*(1205+298*sqrt(5))))/2245) ≈161.946011928 degrees
Dual Solid: Biscribed Truncated Icosahedron
(values below based on circumscribed radius = 1)
Short Edge (60): sqrt(30*(15−sqrt(15*(5+2*sqrt(5)))))/15 ≈0.64085182017098754129
Long Edge (30): (sqrt(15)−sqrt(3))/3 ≈0.71364417954617986388
Long Edge (30)/Short Edge (60)= 1.113586880904497
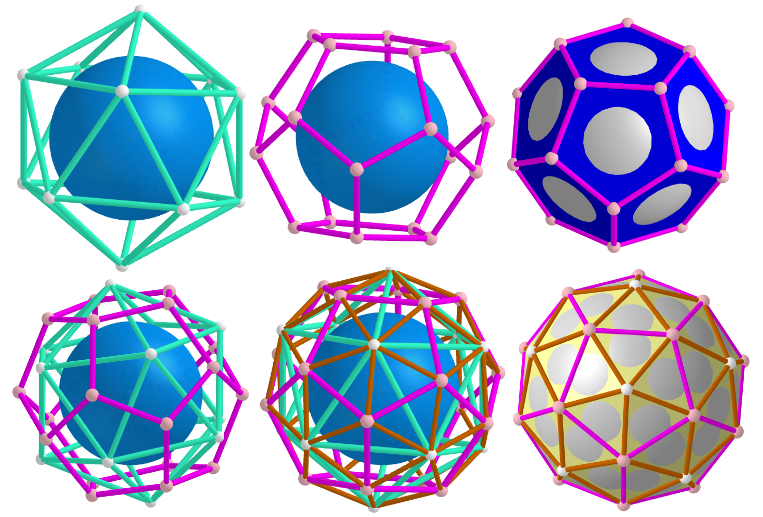
Circumscribed Radius: 1
Inscribed Radius: 1/sqrt(10−sqrt(5)−sqrt(6*(5+sqrt(5)))) ≈0.92260219454398946762
Volume: 2*sqrt(10*(5−sqrt(5)))/3 ≈3.5048740807942240402
Biscribed Pentakis Dodecahedron and its elements
Biscribed Pentakis Dodecahedron and its elements