雪の結晶のような。。。
このワークシートはMath by Codeの一部です。
アート、背景、実装、バリエーションの順に見ていきましょう。
点を動かして、雪の結晶と同じ対称性を感じよう
<タイルの敷き詰め>
タイル敷き詰めは対称性と周期に関係が深いです。
ということは群論とも親和性が高いですね。
1.背景
タイルの敷き詰めは、図形の輪郭や多角形の敷き詰めという視点と
エッシャーの絵で有名な馬や鳥などの模様の平行移動と回転による反復と周期という視点があります。
どちらにしても、「図形要素の入れ替えと対称性」に関係がありますね
要素の入れ替えといえば、
あみだくじ
あみだくじと言えば、
順列。
順列といえば、
対称群Sn
Snと言えば、
群論ですね。
もちろん、群論は対称性に深くかかわります。
でも、いきなり群論ではなく、
正多角形。
合同移動。
群論と模様。
という順番に
「タイルの敷き詰め模様」について考察してみましょう。
正多角形で平面を敷き詰めよう。
・正多角形を1種類だけ使って床をタイル貼りできるのは限られます。
360÷60、360÷90、360÷120は割り切れるので、
正3角形、正4角形、正6角形は1つのカドにあつめられますが、
正5角形は隙間ができたり、重なります。
正7角形以上では360を割り切る内角にはなりません。
内角を考えるよりも、枚数を考えれば即わかります。
正6角形でも3枚あつまるので、正7角形以上でうまくいっても3枚を切ります。ということは2枚か1枚で
360度にすることになります。
2枚あつめて360度にするには1つの内角が180度というありえない角度になるから、絶対無理ですね。
・正多角形を2種類以上使ってよいことにしたらどうでしょうか。
角度の親和性から考えると、正6角形と正3角形はすぐに思いつきやすいですね。
正方形を使うものと使わないものに大きく分類することもできます。
また、正多角形の1外角はN=3~12までで, 整数は、360÷N=120,90,72,60,-, 45,40, 36, -,30。
だから、1内角は180 - 360/N= 60, 90 , 108, 120, 135, 140, 144, 150です。
これらの和が360度になる組み合わせをさがせばよいね。
108, 144は5枚あつめないと5の倍数にならないし、5枚では360を超えるので可能性はありませんね。
また、360は3の倍数だから、140を3枚使わないと3の倍数にならないので使えません。
だから、敷き詰めに使える多角形は
正3角形、正方形、正6角形、正8角形、正12角形です。
1内角は60、90、120、135、150です。すべて15の倍数です。
・念のために、Nが13以上の正N角形を検証する。
Nが13以上で、360の約数になるのは、N=15以上なので、1外角は360÷15=24以下です。
1内角は180-24=156以上の15の倍数です。 あてはまるのは、165だけです。
180- 165=15 , 360÷15=24で、正24角形です。しかし、165は10の倍数ではないので、
360度にするには、165は偶数枚必要です。165×2=330度。残りは360-330=30度ですが、
1つの内角が30度の正多角形はないので、無理です。
結局使える正多角形は5種類だけですね。
正3角形、正方形、
正6角形、正8角形、正12角形です。
1内角は60、90、120、135、150です。すべて15の倍数です。
そこで、少ない角数、小さい内角に着目してさがすことにしよう。
図の書きやすさから、まずは正方形を必ず使う場合に取り組もう。
次に、正三角形を必ず使う場合も考えよう。
質問:正方形と別の正多角形を使った床の敷き詰め例をかいてください。
ただし、頂点のまわりの模様がどこも同じとします。
正方形をあつめると、正方形だけで埋め尽くすのでダメですね。
正方形を3つあつめて、残りが90度ですから、正方形だけになりダメです。
ということは、1つの点にあつまる正方形の数は1個か2個のどちらかです。
<1点に2個の正方形>
1つ目の正方形のとなりあう2つの頂点をA,Bとします。
Aにあつまった正方形の2つの直角と引いた残りは360-90×2=180=60×3から、
正三角形3個をAにくっつけることができます。
もしも、Bにも正三角形3個をくっつけるなら、2点A、Bを共有する正三角形が1個あります。
・もしも、正三角形どうしが連続するなら、Aの周りもBの周りも3個の正三角形がつながるので、
正方形も連続します。
基本図形は正方形1個の向かい合う2辺にそれぞれ、
正三角形を2個ずつくっつけたひし形をつけた5個図形。
それを、水平に正方形の1辺をベクトルとして平行移動してくっつけます。
できた図形の帯を上下に平行移動してくっつけると、敷き詰めができるでしょう。
それが、下の<図1>です。
図1.正方形と正三角形で敷き詰め1
・1点に正方形が2個あつまるときの正三角形3個をかためずに、1個と2個に分けてくっつけることもできそうです。
正方形と2個の正三角形の3個の図形を2組つけたもの基本図形にしよう。
基本図形の向かい合う平行な辺に、別の基本図形の辺が重なるように2方向に平行移動して、
反復しましょう。それが、次の<図2>です。
図2.正方形と正三角形で敷き詰め2
・1点のまわりの正方形2個の残り180度を正三角形3個で埋めるのは図1、図2の2種類ありました。
180=60+120だから、正三角形と正6角形でも埋められます。
正六角形の連続する3つの辺に正方形をくっつけて、正方形3個の間にできた2個の隙間に正三角形をうめた形を基本図形とします。
基本図形の向かい合う平行な辺に、別の基本図形の辺が重なるように2方向に平行移動して、
反復しましょう。それが、次の<図3>です。
図3.正方形と正三角形と正六角形で敷き詰め
<1点に1個の正方形>
360-90=270度を90度以外の正多角形を使ってあつめます。
正方形以外の多角形の角度は
3,6,8,12角形が、60,120,135,150度です。
・270÷2=135。
正方形の1つの頂点に、2つの正8角形があつまっているのができそうだ。
言い換えると、正方形1つを正8角形4個が取り囲む形に敷き詰められている。
正方形1つと正8角形1個を組にしたものが基本図形です。これを2方向に平行移動して反復すると敷き詰められるね。それが、次の<図4>です。
図4.正方形と正8角形
・270=150+120
ここから、正方形の1点に正12角形と正6角形があつまる。
正方形ABCDの辺ABを共有する正12角形とかき、正方形の両となりに正6角形をくっつけ、さらに
正方形をその2つの正6角形にくっつく2つをかきます。この2つの正方形は、下にスライドしてもよいね。これが基本図形です。斜めに左右に平行移動コピーすればよい。これが下の<図5>です。
図5.正方形と正6角形と正12角形
<正方形を使わずに正三角形を使う場合>
質問:正三角形と正方形以外の正多角形で敷き詰めをするにはどう調べればようでしょうか。
1つの点にあつまる正三角形が6、5は除外されるので、次は4,3,2,1の4通りをしらべます。
<1点に4個の正三角形>
正三角形を6-4=2枚減らすと、正六角形1枚で代用できます。
正六角形を基準にみると、1頂点に4枚あつまるので、正三角形に包囲されます。
たとえば、正6角形の連続する4辺だけ正三角形をつけて、間の3か所のうち、2か所に2個ずつ補うと、正三角形を4+2+2=8個つかいます。たとえば、これを基本図形にして平行移動して反復します。それが<図6>です。
図6.正三角形と正6角形
正三角形を1枚だけ減らしても、残りの角度120+60=180度の内角の多角形はないので、
次は2枚減らします。
<1点に2個の正三角形>
残りの角度は、120+60+60=240=120×2なので、1点に正三角形2枚と正6角形2枚をあつめます。
対称性から1点に正三角形と正6角形を交互に並べます。
正6角形の向かい合う2辺に正三角形をつけると、基本図形はひし形になります。
これを平行移動して反復しましょう。それが、<図7>です。
図7.正三角形と正6角形
<1点に1個の正三角形>
1点にあつまる正三角形をさらに1枚へらすと、残りの角度は、240+60=300=150×2なので、
正三角形の1頂点の周りに、正12角形を2つ敷き詰めます。
言い換えると、正12角形をならべていき、3つの正12角形にかこまれるところに正三角形ができるようにします。正12角形1つにつき、1つおきに正三角形を2つつけたものを基本図形にします。それを平行移動して反復します。それが、<図8>です。
図8.正三角形と正8角形
<反復で敷き詰められる多角形>
正方形、長方形に限らず、
平行四辺形は
平行移動を2方向にすれば敷き詰められるのは自明だね。
平行6辺形も敷き詰め可能だ。
(理由)
平行6辺形Tの向かいあう辺をa,b,c とすると、周囲はa,b,c,a,b,cの順につながっている。
そこで、合同なTを複数用意して、aどうしが重なるように1直線につないで帯を作る。
その帯のa以外の辺はb,cが連続するギザギザになり、2つのa以外の周囲の線は合同な折れ線Lになるね。
ということは、帯を複数用意して、折れ線LとLが重なるようにすれば、平面が敷き詰められるね。
2辺が平行な5角形は敷き詰め可能だ。
(理由)
平行6辺形を、対称の中心を通る線で切ると、合同な5角形ができる。
その5角形には平行な2辺が1組だけある。それは、もとの平行6辺形の1組の平行線からくる。
合同な四角形は反復して敷き詰められる。
(理由)
下の図のように、
4つの合同な四角形は同じ長さの辺の中点で点対称にくっつけると平行四辺形(青)の4頂点が作れる。
だから、4つの四角形を組みにしたタイルと考えれば、2方向に平行移動コピーすることで、
敷き詰められるね。
実は、2つで反復の基本図形ができます。同じ長さの辺の中点で2つの合同な四角形をくっけると、周囲の線が、a,b,c,b,cとなります。同じ記号は同じ長さで平行ですから、平行6辺形です。平行6辺形は敷き詰め可能ですら、これで反復できますね。
平行6辺形は辺がa,b,cの3種の長さで3方向
合同な四角形から平行四辺形・平行6辺形をつくる
上述のように、
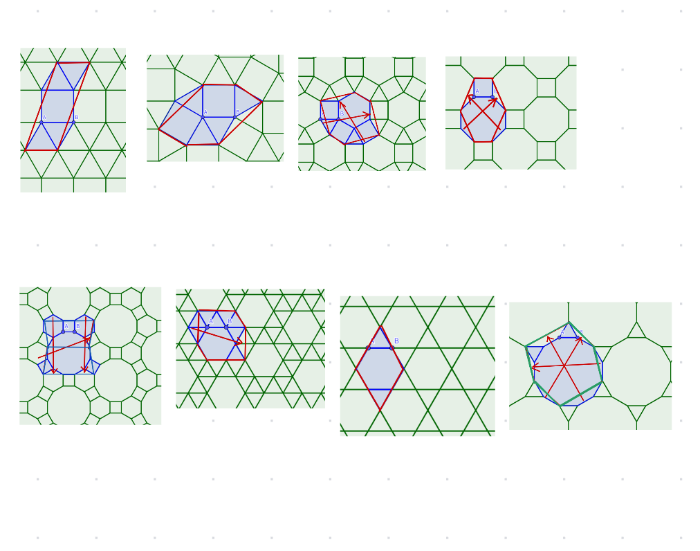
正多角形を2種類以上組わせる敷き詰めは8パターンあったね。
これらを、今の平行移動の考え方と点対称の考え方に基づい見直してみよう。
どれも、基本図形を2方向の平行移動で反復すると敷き詰めができた。
だから、隣接する基本図形どうしの平行な折れ線にそって、単純化をすることで、
平行6辺形、平行4辺形などに変形できることがわかるね。
変形するときの移動方向は、
基本図形の反復のための平行移動の方向ベクトルとして使えるね。
正多角形の敷き詰めの基本図形を単純化してみよう。