Law of Cosines: Open Middle Problem (V1)
Inspired by this Open Middle problem submitted by Erick Lee:
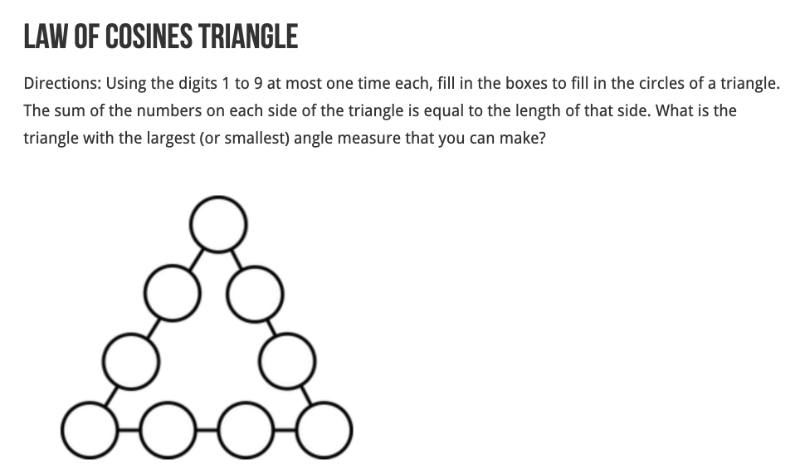
Create different triangle by filling in the input boxes on the left. The sum of the numbers on each side of the triangle = the length of that side. Create a triangle with an interior angle that is as LARGE AS POSSIBLE.
What is the measure of the largest possible angle you can make under this "no repeated values" constraint? What are the side lengths of such a triangle?
Create different triangle by filling in the input boxes on the left. The sum of the numbers on each side of the triangle = the length of that side. Create a triangle with an interior angle that is as SMALL AS POSSIBLE.
What is the measure of the smallest possible angle you can make under this "no repeated values" constraint? What are the side lengths of such a triangle?