EJERCITACIÓN
Teorema: dado un triángulo rectángulo de catetos a y b e hipotenusa h (el lado opuesto al ángulo recto). Entonces,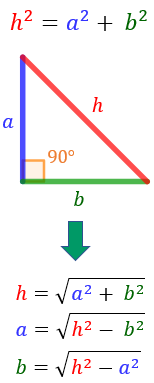 Recordemos que:
Recordemos que: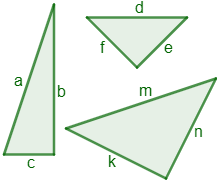 SOLUCIÓN:
Las hipotenusas de los triángulos son los lados aa, dd y mm.
2. Calcular cuánto mide la hipotenusa de un triángulo rectángulo con cuyos catetos miden 33 y 44 centímetros
SOLUCIÓN:
Las hipotenusas de los triángulos son los lados aa, dd y mm.
2. Calcular cuánto mide la hipotenusa de un triángulo rectángulo con cuyos catetos miden 33 y 44 centímetros
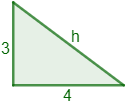 SOLUCIÓN:
Los catetos son a=3a=3 y b=4b=4.Aplicamos el teorema de Pitágoras:h2=a2+b2h2=a2+b2h2=32+42h2=32+42h2=9+16h2=9+16h2=25h2=25Para calcular hh, hacemos la raíz cuadrada:h=+√25h=+25h=5h=5Por tanto, la hipotenusa mide 55 centímetros.3. La Hipotenusa de un triángulo mide √55 y uno de sus catetos mide 22. ¿Cuánto mide el otro cateto?
SOLUCIÓN:
Los catetos son a=3a=3 y b=4b=4.Aplicamos el teorema de Pitágoras:h2=a2+b2h2=a2+b2h2=32+42h2=32+42h2=9+16h2=9+16h2=25h2=25Para calcular hh, hacemos la raíz cuadrada:h=+√25h=+25h=5h=5Por tanto, la hipotenusa mide 55 centímetros.3. La Hipotenusa de un triángulo mide √55 y uno de sus catetos mide 22. ¿Cuánto mide el otro cateto?
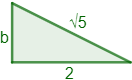 SOLUCIÓN:
La hipotenusa es h=√5h=5 y uno de los catetos es a=2a=2.Aplicamos el teorema de Pitágoras:h2=a2+b2h2=a2+b2(√5)2=22+b2(5)2=22+b2Recordad que el cuadrado de una raíz es el valor absoluto de su radicando (lo de dentro de la raíz, pero con signo positivo), así que (√5)2=5(5)2=5.Continuamos:5=4+b25=4+b2Pasamos el 44 restando al otro lado:5−4=b25−4=b21=b21=b2Para calcular bb, hacemos la raíz cuadrada:b=+√1b=+1b=1b=1Por tanto, el otro cateto mide 11.
4. ¿Cuánto mide la hipotenusa de un triángulo rectángulo cuyos catetos miden 11?
SOLUCIÓN:
La hipotenusa es h=√5h=5 y uno de los catetos es a=2a=2.Aplicamos el teorema de Pitágoras:h2=a2+b2h2=a2+b2(√5)2=22+b2(5)2=22+b2Recordad que el cuadrado de una raíz es el valor absoluto de su radicando (lo de dentro de la raíz, pero con signo positivo), así que (√5)2=5(5)2=5.Continuamos:5=4+b25=4+b2Pasamos el 44 restando al otro lado:5−4=b25−4=b21=b21=b2Para calcular bb, hacemos la raíz cuadrada:b=+√1b=+1b=1b=1Por tanto, el otro cateto mide 11.
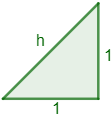
4. ¿Cuánto mide la hipotenusa de un triángulo rectángulo cuyos catetos miden 11?
 SOLUCIÓN:
Los catetos del triángulo son a=1a=1 y b=1b=1.Aplicamos el teorema de Pitágoras para calcula la hipotenusa:h2=a2+b2h2=a2+b2h2=12+12h2=12+12h2=1+1h2=1+1h2=2h2=2Para calcular hh, hacemos la raíz cuadrada:h=+√2h=+2La hipotenusa mide √22 (aproximadamente, 1,411,41).
5. ¿A qué altura está la cometa de Ana si su cuerda mide L=8L=8 metros y tendría que moverse 66 metros para situarse debajo de ella?
SOLUCIÓN:
Los catetos del triángulo son a=1a=1 y b=1b=1.Aplicamos el teorema de Pitágoras para calcula la hipotenusa:h2=a2+b2h2=a2+b2h2=12+12h2=12+12h2=1+1h2=1+1h2=2h2=2Para calcular hh, hacemos la raíz cuadrada:h=+√2h=+2La hipotenusa mide √22 (aproximadamente, 1,411,41).
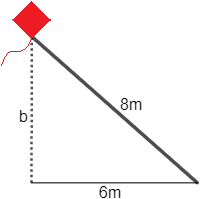
5. ¿A qué altura está la cometa de Ana si su cuerda mide L=8L=8 metros y tendría que moverse 66 metros para situarse debajo de ella?
 SOLUCIÓN:
El ángulo que forma la altura con el suelo es un ángulo recto, con lo que tenemos un triángulo rectángulo.La cuerda es la hipotenusa del triángulo: h=8h=8.La distancia que habría que desplazarse es la base del triángulo, es decir, uno de los catetos: a=6a=6.La altura a la que se encuentra la cometa es el otro cateto: bb.Aplicamos el teorema de Pitágoras:h2=a2+b2h2=a2+b282=62+b282=62+b264=36+b264=36+b2Pasamos 3636 al otro lado:64−36=b264−36=b228=b228=b2Para calcular bb, hacemos la raíz cuadrada:b=+√28b=+28Podemos escribir el número 2828 como un producto para simplificar:b=√7⋅2⋅2b=7·2·2Como hay un 2222, sale de la raíz un 22:b=2√7b=27Se encuentra a 2√727 metros de altura (aproximadamente, 5,29 m5,29 m).
6. ¿Cuánto miden los lados de un cuadrado cuya diagonal mide d=2d=2?
SOLUCIÓN:
El ángulo que forma la altura con el suelo es un ángulo recto, con lo que tenemos un triángulo rectángulo.La cuerda es la hipotenusa del triángulo: h=8h=8.La distancia que habría que desplazarse es la base del triángulo, es decir, uno de los catetos: a=6a=6.La altura a la que se encuentra la cometa es el otro cateto: bb.Aplicamos el teorema de Pitágoras:h2=a2+b2h2=a2+b282=62+b282=62+b264=36+b264=36+b2Pasamos 3636 al otro lado:64−36=b264−36=b228=b228=b2Para calcular bb, hacemos la raíz cuadrada:b=+√28b=+28Podemos escribir el número 2828 como un producto para simplificar:b=√7⋅2⋅2b=7·2·2Como hay un 2222, sale de la raíz un 22:b=2√7b=27Se encuentra a 2√727 metros de altura (aproximadamente, 5,29 m5,29 m).
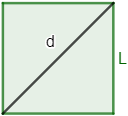
6. ¿Cuánto miden los lados de un cuadrado cuya diagonal mide d=2d=2?
 SOLUCIÓN:
Un cuadrado está formado por dos triángulos rectángulos iguales. La diagonal del cuadrado, dd, es la hipotenusa de los triángulos.Como se trata de un cuadrado, sus cuatro lados miden lo mismo, LL. Así, los catetos de los triángulos también miden LL.Aplicamos el teorema de Pitágoras:d2=L2+L2d2=L2+L222=L2+L222=L2+L24=2⋅L24=2·L2Pasamos el 22 dividiendo al otro lado:42=L242=L22=L22=L2Hacemos la raíz cuadrada:L=+√2L=+2Por tanto, los lados del cuadrado miden √22 (aproximadamente, 1,411,41).
7. Calcular la hipotenusa de un triángulo rectángulo de base b=6 mb=6 m y área A=9 m2A=9 m2.
SOLUCIÓN:
Un cuadrado está formado por dos triángulos rectángulos iguales. La diagonal del cuadrado, dd, es la hipotenusa de los triángulos.Como se trata de un cuadrado, sus cuatro lados miden lo mismo, LL. Así, los catetos de los triángulos también miden LL.Aplicamos el teorema de Pitágoras:d2=L2+L2d2=L2+L222=L2+L222=L2+L24=2⋅L24=2·L2Pasamos el 22 dividiendo al otro lado:42=L242=L22=L22=L2Hacemos la raíz cuadrada:L=+√2L=+2Por tanto, los lados del cuadrado miden √22 (aproximadamente, 1,411,41).
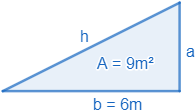
7. Calcular la hipotenusa de un triángulo rectángulo de base b=6 mb=6 m y área A=9 m2A=9 m2.
 SOLUCIÓN:
El área de un triángulo es la mitad de la base, bb, por la altura, aa:A=b⋅a2A=b⋅a2Como el área es 99 y base mide 66, tenemos9=6⋅a29=6⋅a2Resolvemos la ecuación:9=6⋅a29=6⋅a29⋅2=6⋅a9·2=6⋅a18=6⋅a18=6·aa=186=3a=186=3Por tanto, la altura mide 33 metros.Como la base y la altura son los catetos del triángulo, podemos calcular cuánto mide la hipotenusa por el teorema de Pitágoras:h2=a2+b2h2=a2+b2h2=32+62h2=32+62h2=9+36=45h2=9+36=45h=+√45h=+45h=+√3⋅3⋅5h=+3·3·5h=3⋅√5h=3·5Por tanto, la hipotenusa del triángulo mide 3√535 metros (aproximadamente, 6,76,7).
8. Al atardecer, un árbol proyecta una sombra de 2,5 metros de longitud. Si la distancia desde la parte más alta del árbol al extremo más alejado de la sombra es de 4 metros, ¿cuál es la altura del árbol?
SOLUCIÓN:
El área de un triángulo es la mitad de la base, bb, por la altura, aa:A=b⋅a2A=b⋅a2Como el área es 99 y base mide 66, tenemos9=6⋅a29=6⋅a2Resolvemos la ecuación:9=6⋅a29=6⋅a29⋅2=6⋅a9·2=6⋅a18=6⋅a18=6·aa=186=3a=186=3Por tanto, la altura mide 33 metros.Como la base y la altura son los catetos del triángulo, podemos calcular cuánto mide la hipotenusa por el teorema de Pitágoras:h2=a2+b2h2=a2+b2h2=32+62h2=32+62h2=9+36=45h2=9+36=45h=+√45h=+45h=+√3⋅3⋅5h=+3·3·5h=3⋅√5h=3·5Por tanto, la hipotenusa del triángulo mide 3√535 metros (aproximadamente, 6,76,7).
8. Al atardecer, un árbol proyecta una sombra de 2,5 metros de longitud. Si la distancia desde la parte más alta del árbol al extremo más alejado de la sombra es de 4 metros, ¿cuál es la altura del árbol?
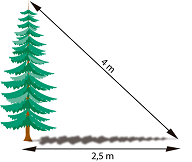 SOLUCIÓN:
Imaginamos un triángulo rectángulo de modo que
SOLUCIÓN:
Imaginamos un triángulo rectángulo de modo que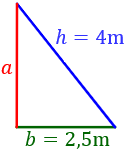 Como el triángulo es rectángulo, aplicamos el teorema de Pitágoras para calcular su altura, aa:
Como el triángulo es rectángulo, aplicamos el teorema de Pitágoras para calcular su altura, aa: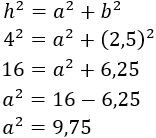 Finalmente, hacemos la raíz cuadrada:
Finalmente, hacemos la raíz cuadrada: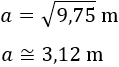 Por tanto, la altura del árbol es, aproximadamente, 3,12 metros.
Por tanto, la altura del árbol es, aproximadamente, 3,12 metros.
 Recordemos que:
Recordemos que:- el triángulo es rectángulo porque tiene un ángulo recto, es decir, un ángulo de 90 grados ó π / 2 radianes.
- la hipotenusa es el lado opuesto al ángulo recto
 SOLUCIÓN:
Las hipotenusas de los triángulos son los lados aa, dd y mm.
2. Calcular cuánto mide la hipotenusa de un triángulo rectángulo con cuyos catetos miden 33 y 44 centímetros
SOLUCIÓN:
Las hipotenusas de los triángulos son los lados aa, dd y mm.
2. Calcular cuánto mide la hipotenusa de un triángulo rectángulo con cuyos catetos miden 33 y 44 centímetros
 SOLUCIÓN:
Los catetos son a=3a=3 y b=4b=4.Aplicamos el teorema de Pitágoras:h2=a2+b2h2=a2+b2h2=32+42h2=32+42h2=9+16h2=9+16h2=25h2=25Para calcular hh, hacemos la raíz cuadrada:h=+√25h=+25h=5h=5Por tanto, la hipotenusa mide 55 centímetros.3. La Hipotenusa de un triángulo mide √55 y uno de sus catetos mide 22. ¿Cuánto mide el otro cateto?
SOLUCIÓN:
Los catetos son a=3a=3 y b=4b=4.Aplicamos el teorema de Pitágoras:h2=a2+b2h2=a2+b2h2=32+42h2=32+42h2=9+16h2=9+16h2=25h2=25Para calcular hh, hacemos la raíz cuadrada:h=+√25h=+25h=5h=5Por tanto, la hipotenusa mide 55 centímetros.3. La Hipotenusa de un triángulo mide √55 y uno de sus catetos mide 22. ¿Cuánto mide el otro cateto?
 SOLUCIÓN:
La hipotenusa es h=√5h=5 y uno de los catetos es a=2a=2.Aplicamos el teorema de Pitágoras:h2=a2+b2h2=a2+b2(√5)2=22+b2(5)2=22+b2Recordad que el cuadrado de una raíz es el valor absoluto de su radicando (lo de dentro de la raíz, pero con signo positivo), así que (√5)2=5(5)2=5.Continuamos:5=4+b25=4+b2Pasamos el 44 restando al otro lado:5−4=b25−4=b21=b21=b2Para calcular bb, hacemos la raíz cuadrada:b=+√1b=+1b=1b=1Por tanto, el otro cateto mide 11.
4. ¿Cuánto mide la hipotenusa de un triángulo rectángulo cuyos catetos miden 11?
SOLUCIÓN:
La hipotenusa es h=√5h=5 y uno de los catetos es a=2a=2.Aplicamos el teorema de Pitágoras:h2=a2+b2h2=a2+b2(√5)2=22+b2(5)2=22+b2Recordad que el cuadrado de una raíz es el valor absoluto de su radicando (lo de dentro de la raíz, pero con signo positivo), así que (√5)2=5(5)2=5.Continuamos:5=4+b25=4+b2Pasamos el 44 restando al otro lado:5−4=b25−4=b21=b21=b2Para calcular bb, hacemos la raíz cuadrada:b=+√1b=+1b=1b=1Por tanto, el otro cateto mide 11.
4. ¿Cuánto mide la hipotenusa de un triángulo rectángulo cuyos catetos miden 11?
 SOLUCIÓN:
Los catetos del triángulo son a=1a=1 y b=1b=1.Aplicamos el teorema de Pitágoras para calcula la hipotenusa:h2=a2+b2h2=a2+b2h2=12+12h2=12+12h2=1+1h2=1+1h2=2h2=2Para calcular hh, hacemos la raíz cuadrada:h=+√2h=+2La hipotenusa mide √22 (aproximadamente, 1,411,41).
5. ¿A qué altura está la cometa de Ana si su cuerda mide L=8L=8 metros y tendría que moverse 66 metros para situarse debajo de ella?
SOLUCIÓN:
Los catetos del triángulo son a=1a=1 y b=1b=1.Aplicamos el teorema de Pitágoras para calcula la hipotenusa:h2=a2+b2h2=a2+b2h2=12+12h2=12+12h2=1+1h2=1+1h2=2h2=2Para calcular hh, hacemos la raíz cuadrada:h=+√2h=+2La hipotenusa mide √22 (aproximadamente, 1,411,41).
5. ¿A qué altura está la cometa de Ana si su cuerda mide L=8L=8 metros y tendría que moverse 66 metros para situarse debajo de ella?
 SOLUCIÓN:
El ángulo que forma la altura con el suelo es un ángulo recto, con lo que tenemos un triángulo rectángulo.La cuerda es la hipotenusa del triángulo: h=8h=8.La distancia que habría que desplazarse es la base del triángulo, es decir, uno de los catetos: a=6a=6.La altura a la que se encuentra la cometa es el otro cateto: bb.Aplicamos el teorema de Pitágoras:h2=a2+b2h2=a2+b282=62+b282=62+b264=36+b264=36+b2Pasamos 3636 al otro lado:64−36=b264−36=b228=b228=b2Para calcular bb, hacemos la raíz cuadrada:b=+√28b=+28Podemos escribir el número 2828 como un producto para simplificar:b=√7⋅2⋅2b=7·2·2Como hay un 2222, sale de la raíz un 22:b=2√7b=27Se encuentra a 2√727 metros de altura (aproximadamente, 5,29 m5,29 m).
6. ¿Cuánto miden los lados de un cuadrado cuya diagonal mide d=2d=2?
SOLUCIÓN:
El ángulo que forma la altura con el suelo es un ángulo recto, con lo que tenemos un triángulo rectángulo.La cuerda es la hipotenusa del triángulo: h=8h=8.La distancia que habría que desplazarse es la base del triángulo, es decir, uno de los catetos: a=6a=6.La altura a la que se encuentra la cometa es el otro cateto: bb.Aplicamos el teorema de Pitágoras:h2=a2+b2h2=a2+b282=62+b282=62+b264=36+b264=36+b2Pasamos 3636 al otro lado:64−36=b264−36=b228=b228=b2Para calcular bb, hacemos la raíz cuadrada:b=+√28b=+28Podemos escribir el número 2828 como un producto para simplificar:b=√7⋅2⋅2b=7·2·2Como hay un 2222, sale de la raíz un 22:b=2√7b=27Se encuentra a 2√727 metros de altura (aproximadamente, 5,29 m5,29 m).
6. ¿Cuánto miden los lados de un cuadrado cuya diagonal mide d=2d=2?
 SOLUCIÓN:
Un cuadrado está formado por dos triángulos rectángulos iguales. La diagonal del cuadrado, dd, es la hipotenusa de los triángulos.Como se trata de un cuadrado, sus cuatro lados miden lo mismo, LL. Así, los catetos de los triángulos también miden LL.Aplicamos el teorema de Pitágoras:d2=L2+L2d2=L2+L222=L2+L222=L2+L24=2⋅L24=2·L2Pasamos el 22 dividiendo al otro lado:42=L242=L22=L22=L2Hacemos la raíz cuadrada:L=+√2L=+2Por tanto, los lados del cuadrado miden √22 (aproximadamente, 1,411,41).
7. Calcular la hipotenusa de un triángulo rectángulo de base b=6 mb=6 m y área A=9 m2A=9 m2.
SOLUCIÓN:
Un cuadrado está formado por dos triángulos rectángulos iguales. La diagonal del cuadrado, dd, es la hipotenusa de los triángulos.Como se trata de un cuadrado, sus cuatro lados miden lo mismo, LL. Así, los catetos de los triángulos también miden LL.Aplicamos el teorema de Pitágoras:d2=L2+L2d2=L2+L222=L2+L222=L2+L24=2⋅L24=2·L2Pasamos el 22 dividiendo al otro lado:42=L242=L22=L22=L2Hacemos la raíz cuadrada:L=+√2L=+2Por tanto, los lados del cuadrado miden √22 (aproximadamente, 1,411,41).
7. Calcular la hipotenusa de un triángulo rectángulo de base b=6 mb=6 m y área A=9 m2A=9 m2.
 SOLUCIÓN:
El área de un triángulo es la mitad de la base, bb, por la altura, aa:A=b⋅a2A=b⋅a2Como el área es 99 y base mide 66, tenemos9=6⋅a29=6⋅a2Resolvemos la ecuación:9=6⋅a29=6⋅a29⋅2=6⋅a9·2=6⋅a18=6⋅a18=6·aa=186=3a=186=3Por tanto, la altura mide 33 metros.Como la base y la altura son los catetos del triángulo, podemos calcular cuánto mide la hipotenusa por el teorema de Pitágoras:h2=a2+b2h2=a2+b2h2=32+62h2=32+62h2=9+36=45h2=9+36=45h=+√45h=+45h=+√3⋅3⋅5h=+3·3·5h=3⋅√5h=3·5Por tanto, la hipotenusa del triángulo mide 3√535 metros (aproximadamente, 6,76,7).
8. Al atardecer, un árbol proyecta una sombra de 2,5 metros de longitud. Si la distancia desde la parte más alta del árbol al extremo más alejado de la sombra es de 4 metros, ¿cuál es la altura del árbol?
SOLUCIÓN:
El área de un triángulo es la mitad de la base, bb, por la altura, aa:A=b⋅a2A=b⋅a2Como el área es 99 y base mide 66, tenemos9=6⋅a29=6⋅a2Resolvemos la ecuación:9=6⋅a29=6⋅a29⋅2=6⋅a9·2=6⋅a18=6⋅a18=6·aa=186=3a=186=3Por tanto, la altura mide 33 metros.Como la base y la altura son los catetos del triángulo, podemos calcular cuánto mide la hipotenusa por el teorema de Pitágoras:h2=a2+b2h2=a2+b2h2=32+62h2=32+62h2=9+36=45h2=9+36=45h=+√45h=+45h=+√3⋅3⋅5h=+3·3·5h=3⋅√5h=3·5Por tanto, la hipotenusa del triángulo mide 3√535 metros (aproximadamente, 6,76,7).
8. Al atardecer, un árbol proyecta una sombra de 2,5 metros de longitud. Si la distancia desde la parte más alta del árbol al extremo más alejado de la sombra es de 4 metros, ¿cuál es la altura del árbol?
 SOLUCIÓN:
Imaginamos un triángulo rectángulo de modo que
SOLUCIÓN:
Imaginamos un triángulo rectángulo de modo que- su base, bb, es la sombra del árbol,
- su altura, aa, es la altura del árbol y
- su hipotenusa, hh, es la distancia desde el árbol al extremo de la sombra.
 Como el triángulo es rectángulo, aplicamos el teorema de Pitágoras para calcular su altura, aa:
Como el triángulo es rectángulo, aplicamos el teorema de Pitágoras para calcular su altura, aa: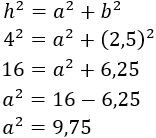 Finalmente, hacemos la raíz cuadrada:
Finalmente, hacemos la raíz cuadrada: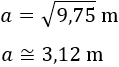 Por tanto, la altura del árbol es, aproximadamente, 3,12 metros.
Por tanto, la altura del árbol es, aproximadamente, 3,12 metros.