gebrochen-rationale Funktionen
Einführungsvideo
Mit folgendem Applet können Sie das Verhalten einer einfachen gebrochen-rationalen Funktion an der Polstelle nachvollziehen:
- Verändern Sie den Schieberegler der Nullstelle und beobachten Sie, wie die Polstelle und die senkrechte Asymptote wandert!
- Verändern Sie den Schieberegler der Vielfachheit der Nullstelle und beobachten Sie, wie sich das "Richtungsverhalten" an der Polstelle verändert.
- Verändern Sie den Zähler der Funktion und beobacheten Sie, wie sich die Funktion an sich ändert, aber die Polstelle, die senkrechte Asymptote oder das prinzipielle Richtungsverhalten sich nicht ändern!
Applet zu Asymptoten und Polstellen
Mit folgendem Applet können Sie das Verhalten einer gebrochen-rationalen Funktion im Unendlichen nachvollziehen:
- Verändern Sie den Schieberegler für Zähler- und Nennergrad und beobachten Sie die Auswirkungen auf den Graphen im Unendlichen!
- Verändern Sie für den Fall, dass Zähler- und Nennergrad übereinstimmen die Zahlen an und bn (also die Zahlen vor der höchsten Potenz in Zähler bzw. Nenner) und beobachen die Auswirkungen auf den Graphen.
Beispiel zum Zeichnen
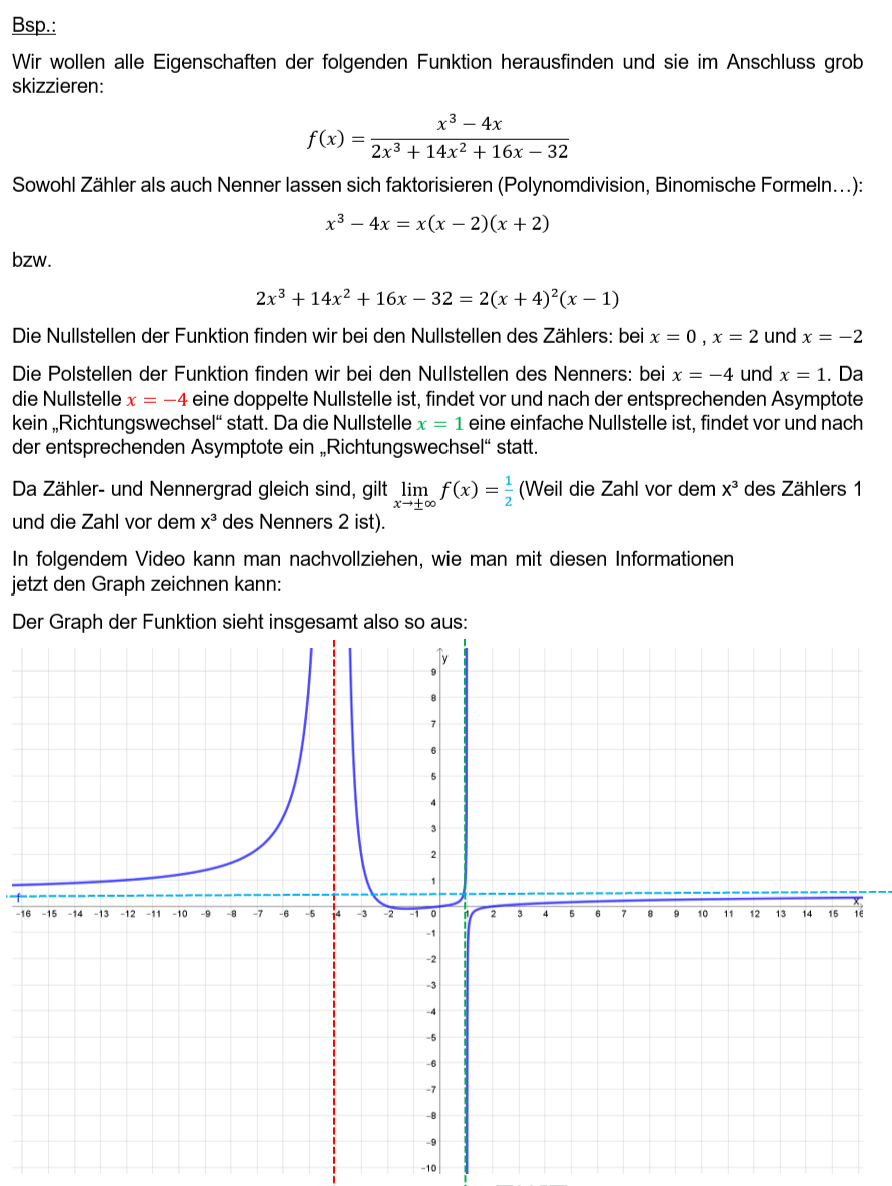
Mit folgendem Applet können Sie beliebig oft üben, eine gebrochen-rationale Funktion zu zeichnen. Die Grün hinterlegten Schriftzüge können gedrückt werden!