Função do Segundo Grau
Questão 1
A função que tem 2 e 3 como raízes reais é
Questão 2
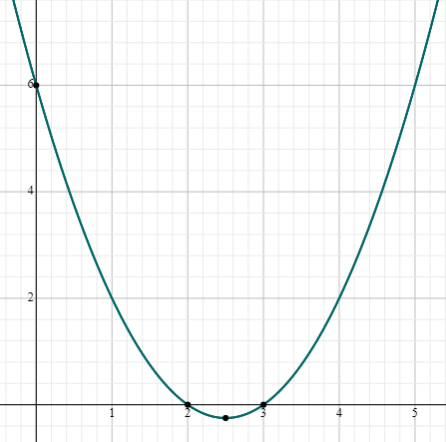
Observe a figura acima e responda
O valor máximo que a função assume em todo seu domínio é 6
O valor mínimo que a função assume está no intervalo (2,3)
Questão 3
A animação abaixo está representada pelo gráfico da função f(x)=ax²+bx+c, onde os valores de b e c estão fixados em. O valor de a varia entre -20 e 20. Observe o movimento na animação e de acordo com a variação de a responda as perguntas.
O que acontece quando o valor de a se aproxima de zero?
Qual característica semelhante a função apresenta quando a tende para +∞ e -∞?
Questão 4
A animação abaixo está representada pelo gráfico da função f(x)=ax²+bx+c, onde os valores de a e c estão fixados em. O valor de b varia entre -20 e 20. Observe o movimento na animação e de acordo com a variação de b e responda as perguntas.
Observe o gráfico abaixo.
O que acontece com a função quando b tende a -∞? E a +∞?
O valor máximo que o vértice da parábola atinge é quando b=0.
Questão 5
A animação abaixo está representada pelo gráfico da função f(x)=ax²+bx+c, onde os valores de a e b estão fixados. O valor de c varia entre -5 e 5. Observe o movimento na animação e de acordo com a variação de c e responda as perguntas.
O que acontece com a função quando c varia?
É possível afirmar que a função tem um único valor máximo ou um único mínimo independente do valor de c?
Questão 6
Na questão abaixo: deslize o ponto A na função f(azul). Você observa que que a função g(preta) vai se deslocar.
A função g é chamada de função tangente. Nesse caso, dizemos que ela é tangente a f. Responda as perguntas abaixo.
A função g quando x<0 é
A função g quando x>0 é
O que acontece com a reta tangente g quando A=(0,0)?