circles and bundles of radii
- Author:
- chris cambré
- Topic:
- Circle
starting with radii
The girih method working with a fixed set of polygons creates stars with a fixed number of points. I addition to this system a second method was established. In circle bundles of radii were drawn. Intersection points of these radii define segments, forming polygons. This construction method allows combining stars with a different number of points within one pattern. In the article Girih for Domes: Analysis of Three Iranian Domes the authors Mohammad Hossein Kasraei, Yahya Nourian and Mohamadjavad Mahdavinejad describe this method as the radial girih method or Dast-Gardan girih.
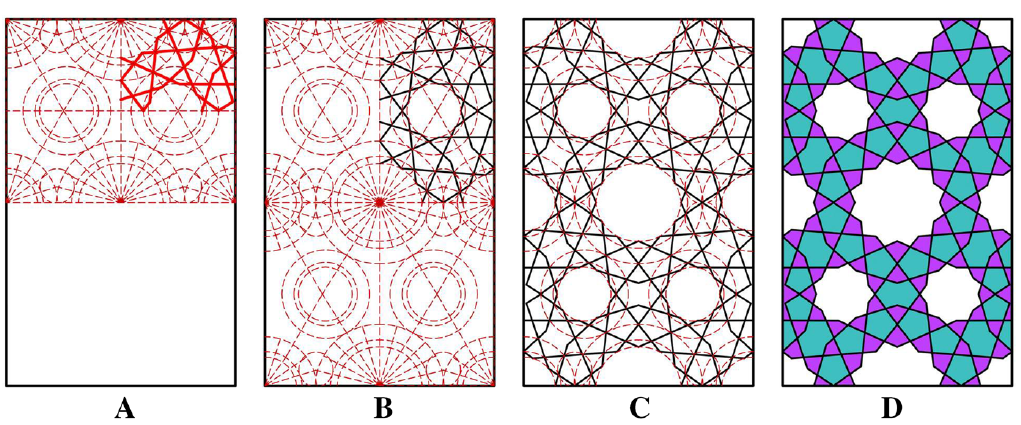
In the example you can see how the pattern is constructed.
- Within a unit repeat concentric circles are drawn on every corner point.
- These circles are divided into congruent sectors.
- Diagonals in the unit repeat define the center points of additional circles (step A).
- Connecting intersection points of radii and circles generates a line pattern (step B).
- This pattern is mirrored on the axes of symmetry if the unit repeat (step C).
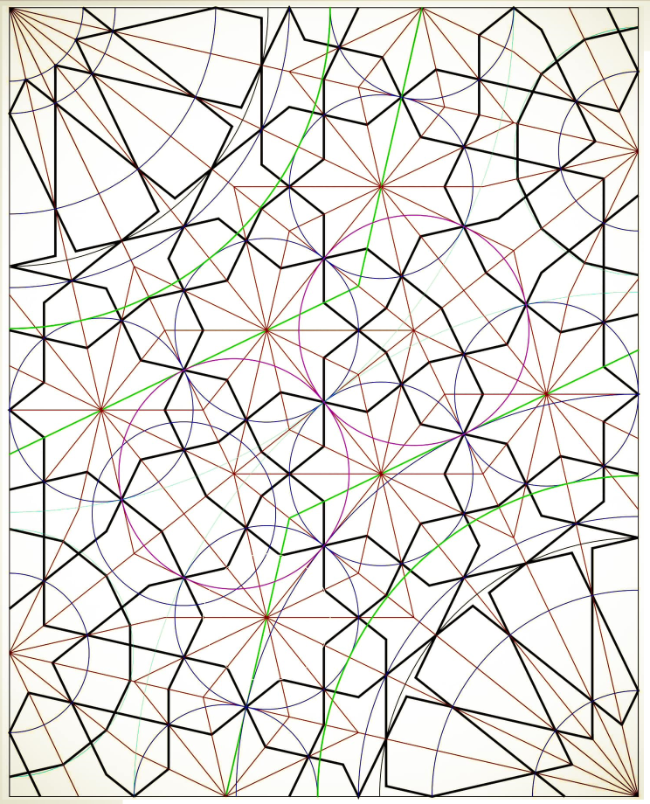
A nice example is shown in a drawing by Aslam Qureshi.
The construction starts with two quart circles in opposed corners of a rectangle and smaller, tangent circles. With bundles of radii and intersections points a balanced 7-fold pattern is created.
