L2.1 - Congruent Parts, Part 1
Learning Intentions and Success Criteria
- Determine whether or not figures are congruent by reasoning about rigid transformations (in writing).
- Generate and comprehend congruence statements (orally and in writing) that establish corresponding parts.
- Identify corresponding parts from a congruence statement.
- Use rigid transformations to figure out if figures are congruent.
- Write a congruence statement.
1.1: Notice and Wonder: Transformed Rectangles
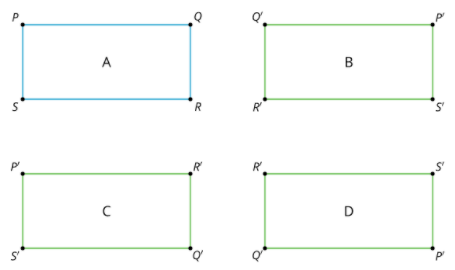
What do you notice? What do you wonder?
1.2: If We Know This, Then We Know That...
Triangle ABC is congruent to triangle DEF.
ABC DEF 1. Find a sequence of rigid motions that takes triangle ABC to triangle DEF.
2. What is the image of segment BC after that transformation?
3. Explain how you know those segments are congruent.
4. Justify that angle ABC is congruent to angle DEF.
1.2: Are You Ready For More?
For each figure, draw additional line segments to divide the figure into 2 congruent polygons. Label any new vertices and identify the corresponding vertices of the congruent polygons.
1.3: Making Quadrilaterals
1. Draw a triangle. 2. Find the midpoint of the longest side of your triangle. 3. Rotate your triangle 180 using the midpoint of the longest side as the center of the rotation. 4. Label the corresponding parts and mark what must be congruent. 5. Make a conjecture and justify it. a. What type of quadrilateral have you formed?
b. What is the definition of that quadrilateral type?
c. Why must the quadrilateral you have fit the definition?
Lesson Synthesis: Congruent Parts, Part 1
Write down your reason for why corresponding parts of congruent figures must be congruent.

Learning Intentions and Success Criteria
- Determine whether or not figures are congruent by reasoning about rigid transformations (in writing).
- Generate and comprehend congruence statements (orally and in writing) that establish corresponding parts.
- Identify corresponding parts from a congruence statement.
- Use rigid transformations to figure out if figures are congruent.
- Write a congruence statement.
Cool-Down: Making Angle Bisectors
Triangle A’B’C’ is a reflection of triangle ABC across line BC. Prove that ray BC is the angle bisector of angle ABA’.
