Ecuaciones logarítmicas
En esta página explicamos qué es una ecuación logarítmica y resolvemos tres ecuaciones. Es necesario conocer las propiedades de los logaritmos, el cambio de base de los logaritmos y las propiedades de las potencias.
1. Introducción
Una ecuación logarítmica es una ecuación cuya incógnita (o incógnitas) se encuentra multiplicando o dividiendo a los logaritmos, en sus bases o en el argumento de los logaritmos (dentro de los logaritmos).
Ejemplos de ecuaciones logarítmicas:
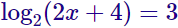La solución es x = 2.
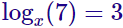La solución es x = raíz cúbica de 7.
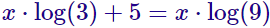La solución es x = 5/log(3).
Como ya dijimos anteriormente, para poder resolver ecuaciones logarítmicas, necesitamos conocer las propiedades de los logaritmos(incluyendo el cambio de base) y las propiedades de las potencias.
- Incógnita en el argumento:
La solución es x = 2.
- Incógnita en la base:
La solución es x = raíz cúbica de 7.
- Incógnita multiplicando al logaritmo:
La solución es x = 5/log(3).
Como ya dijimos anteriormente, para poder resolver ecuaciones logarítmicas, necesitamos conocer las propiedades de los logaritmos(incluyendo el cambio de base) y las propiedades de las potencias.2. Ecuaciones logarítmicas resueltas
El método que vamos a seguir es operar en la ecuación hasta obtener, si es posible, una igualdad entre dos logaritmos en la misma base (si no se indica, consideramos que la base es 10):
Llegados a este punto, podemos, lógicamente, igualar los argumentos de los logaritmos:
Para terminar, comprobamos que la solución obtenida no hace que los argumentos de los logaritmos de la ecuación inicial sean no positivos (porque éstos deben ser siempre positivos).
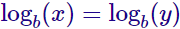Llegados a este punto, podemos, lógicamente, igualar los argumentos de los logaritmos:
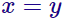Para terminar, comprobamos que la solución obtenida no hace que los argumentos de los logaritmos de la ecuación inicial sean no positivos (porque éstos deben ser siempre positivos).Ecuación 1
Solución:
Como la suma de logaritmos es el logaritmo del producto,
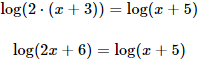Como ya tenemos una igualdad entre dos logaritmos en la misma base, igualamos sus argumentos:
Resolvemos la ecuación de primer grado:
Por tanto, la solución es x=-1.
Para terminar, comprobamos que los argumentos son positivos:
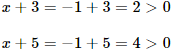
Ecuación 2
Solución:
Recordad que un número que multiplica a un logaritmo puede escribirse como el exponente de su argumento:
Igualamos argumentos:
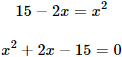Resolvemos la ecuación de segundo grado completa:
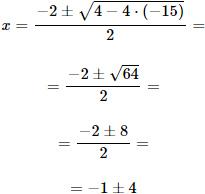Tenemos dos soluciones: x=3 y x=-5.
La segunda solución (la negativa) no es buena porque hace que el argumento del logaritmo del lado derecho de la ecuación sea negativo.La solución de la ecuación logarítmica es x=3.Ecuación 3
Solución:
Como la incógnita está en la base del logaritmo, tiene que ser positiva y distinta de 1.Para resolver esta ecuación, aplicamos un cambio de base en el logaritmo. Recordad la fórmula para cambiar la base:
Cambiamos a base 7:
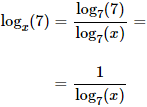Por tanto, tenemos la ecuación logarítmica
Pasamos el denominador al otro lado:
Escribimos el 3 en el argumento:
Escribimos el 1 como un logaritmo en base 7:
Igualamos argumentos y resolvemos la ecuación:
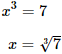El argumento del logaritmo es positivo para esta solución, así que hemos hallado la solución de la ecuación logarítmica.
Más ecuaciones logarítmicas resueltas: