Exponential Equations
An exponential equation is one that has exponential expressions, in other words, powers that have in their exponent expressions with the unknown factor x. For example,
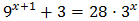
In this paper, we will resolve the exponential equations without using logarithms. This method of resolution consists in reaching an equality of the exponentials with the same base in order to equal the exponents.
In this paper, we will resolve the exponential equations without using logarithms. This method of resolution consists in reaching an equality of the exponentials with the same base in order to equal the exponents.
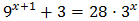
In this paper, we will resolve the exponential equations without using logarithms. This method of resolution consists in reaching an equality of the exponentials with the same base in order to equal the exponents.
In this paper, we will resolve the exponential equations without using logarithms. This method of resolution consists in reaching an equality of the exponentials with the same base in order to equal the exponents.
1. Remember...
Before we start, let's remember the properties of powers:
Product
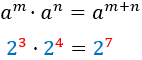
Quocient
Quocient
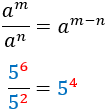
Inverse
Inverse
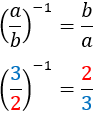
Power
Power
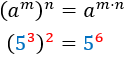
Negative exponent
Negative exponent
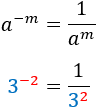
Inverse of inverse
Inverse of inverse
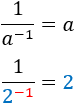
2. Solved equations
Equation 1
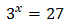
Taking into account that , we can rewrite the equation as
Taking into account that , we can rewrite the equation as
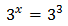
Therefore, the solution is .
Therefore, the solution is . Equation 2
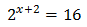
Taking into account that , we can rewrite the equation as
Taking into account that , we can rewrite the equation as
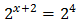
Then we have the linear equation . Therefor, the solution is .
Then we have the linear equation . Therefor, the solution is . Equation 3
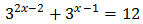
Taking into account that
Taking into account that
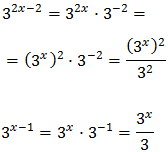
We can rewrite the equation as
We can rewrite the equation as
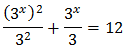
We have the common base , but because one of them is squared, we write
We have the common base , but because one of them is squared, we write
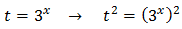
Substituting, the equation finishes like
Substituting, the equation finishes like
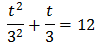
In other words, a quadratic equation:
In other words, a quadratic equation:
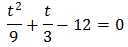 We multiply the full equation by 9:
We multiply the full equation by 9:
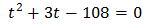
We solve it:
We solve it:
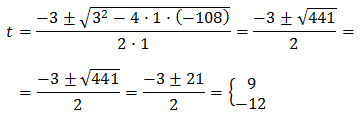
Therefore,
Therefore,
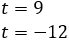 So, we obtain
So, we obtain
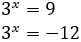
The second option is not possible because it is negative. Therefore,
The second option is not possible because it is negative. Therefore,
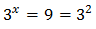
From where we obtain the only one solution .
From where we obtain the only one solution .More examples:
Matesfacil.com by J. Llopis is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License.
Matesfacil.com by J. Llopis is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License.