Natural Space-time in Mixed Coordinate System
From Common space-time to Proper space-time
In physics, we're used to the common space-time (Com) that is shared between all objects and subjects. From Newton, in classic mechanics, it's convenient for us to have a common ruler to measure position of everything and a common clock to attach timestamp onto every event. Then in Relativity Theory, Einstein acknowledged that the space-time structure is different between reference frames of different velocities. So, beside the common space-time that we may all agree to take as the common reference, eg. UTC on Earth, each reference frame moving at velocity v relative to the common space-time does have another space-time which appears to us in the common space-time that "its clock runs slower" and "its ruler is shorter". However, the subjects in that different space-time does not feel any strangeness, the measurement of their objects using their "slower clock" and "shorter ruler" still results in the same physical laws as ours on Earth. That means their slowness and shortness that we see are just apparent effect, and their "slower clock" and "short ruler" are proper, are true to them, thus their space-time measured by those instruments is their proper space-time.
And now the Natural space-time
Look straight into the nature of space and time, we can see that they are not only different but opposite and complement to each other:
- Space is an extrinsic feature reflecting the external state, i.e. the relation between objects.
- Time is an intrinsic feature reflecting the internal state of each individual object.
The natural space-time comprises common space (s) and proper (private) time (τ).
The natural space-time (Nat) has many beautiful properties:
- Natural angle of motion, ϕ, is defined as the angle between the motion vector and the proper time axis in Nat. It's related with θ, the angle of motion in Com, and with ζ, the rapidity of motion, in the the following equations:
- Space & time components of c, the universal speed, AKA. "the speed of light": The natural angle of motion ϕ shows how much the motion is in space versus how much the motion is in time:
- is the speed of motion in space, and
- is the speed of motion in time. So,
- the total speed of motion in Nat is a constant, c.
- Natural velocity ("υ" is upsilon, not vee "v") is unbounded just like how we naturally feel that we can go as fast as we want, not to be limited by c like vs in Com!
- Simple formula for momentum: Just as in classic mechanics (non-relativistic), the momentum is so simple, both in form "p = mυ" and in content where m is the rest mass, thus a constant, not the relativistic mass mrel = m*γ. The relativistic factor γ (Lorentz factor) can be retrieved in Nat with the following equations:
Mixed coordinate system
Fusing both natural space-time and common space-time, we have the mixed coordinate system of 3 axes: common space (s), propertime (τ) and common time (t), with the light cone relates them all together. (See 3D interactive sketch MixedCoords)
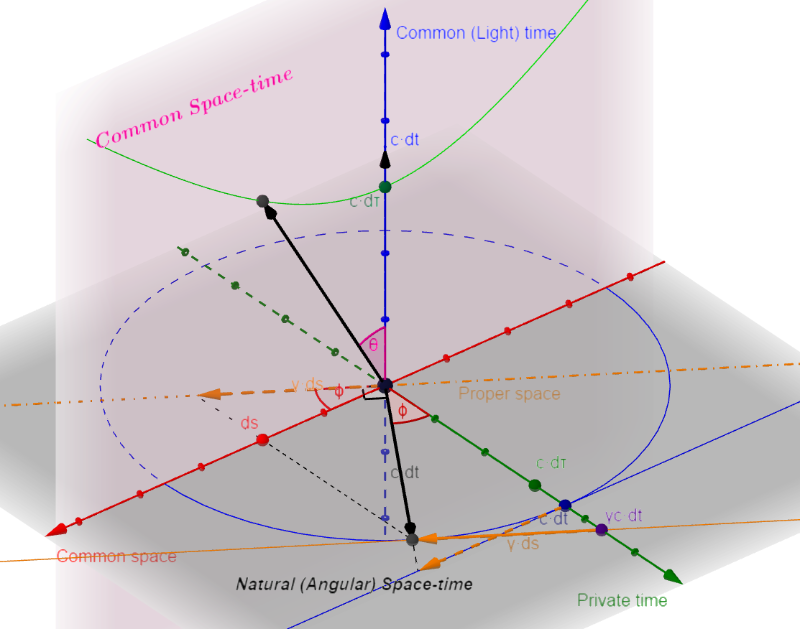
There, we can see that the proper space-time is just the natural space-time rotated by the natural angle of motion ϕ with proper time scaled by the relativistic factor γ while proper space is not scaled.