Eukleidovo odvození objemu jehlanu
Věta: Objem jehlanu je jednou třetinou objemu kvádru se stejnou podstavou i výškou.
Obecný vztah mezi objemem jehlanu a kvádru odvodíme rozpadem kvádru na šest trojbokých jehlanů stejného objemu.
Nejprve kvádr rozřízneme na dva trojboké hranoly stejných objemů a potom každý hranol rozdělíme na tři pravoúhlé trojboké jehlany. Na obrázku je ponechán červený trojboký hranol, druhá polovina je rozdělena na trojboké jehlany (žlutý, červený a modrý).
My víme, že tyto jehlany mají shodné objemy, protože mají shodné podstavy a výšky, ale dokázat tuto větu není vůbec jednoduché. Démokritos z Abdér svou atomistickou teorií postupoval podle mnohem později formulovaného Cavalieriho principu, stejně jako Archimédés. Ale tyto úvahy byly (zřejmě na popud Platóna) považovány za nevědecké, a tak se řečtí matematikové snažili nalézt důkaz jinou cestou. Nás již dnes nepřekvapí, že jimi používaná exhaustivní metoda je jen jiným přiblížením k infinitesimálnímu počtu než Cavalierieho princip.
Vytvoření modelu
Je obtížné, představit si rozklad kvádru bez vhodných prostorových modelů. Lépe se zkoumají skutečné modely jehlanů - vhodným natočením a porovnáním délek hran snadno nalezneme argumenty pro shodný objem. Vhodnými modeláři jsou Tinkercad, SketchUp či Fusion 360. Všechny zmíněné nástroje jsou pro školy zdarma a podporují výstup pro 3D tiskárnu. Model ve 3D GeoGebře vytvoříte také snadno, ale je třeba skrýt v modelu vrcholy i hrany, protože jejich tloušťka, automaticky přidaná exportováním do stl, by znemožnila přesné seskládání dílů do kvádru.
Pokud nemáte 3D tiskárnu, použijte applet níže pro výtisk sítí tří jehlanů a trojbokého hranolu. Barvy sítí odpovídají barvě tělesa na 3D modelu .
STL model - Sketchfab
Důkaz rovnosti objemů jehlanů bez Cavalieriho principu
Nejprve je třeba dokázat, že dva rovnoběžnostěny, které mají shodnou podstavu a výšku mají i shodný objem (ggb). Poté již můžeme dokázat větu o shodnosti objemů jehlanů. Připomeňme Eukleidovo znění exhaustivní (vyčerpávající) metody, kterou pro důkaz věty využijeme.
Jsou-li dány dvě nestejné veličiny a od větší odečteme její část větší než její polovina a od zbytku opět jeho část větší než jeho polovina a budeme tak činit stále, zbude nějaká veličina, jež bude menší než libovolná kladná veličina.
Věta: Mají-li dva jehlany stejnou podstavu a výšku, mají i shodný objem.
Na obrázku níže jsou dva jehlany o shodných základnách i výškách.
Krok 1: Od každého jehlanu odebereme dle právě dokázané věty trojboké hranoly o stejném objemu. Zbydou nám dva jehlany, které jsou jistě menší, než společně "vyčerpaná" modrá část.
Krok 2: Tyto jehlany opět pět rozložíme stejným způsobem. Zbývají nám na každém jehlanu čtyří malé jehlany, o jejichž objemech nic nevíme.
Takto můžeme pokračovat dál, až je rozdíl menší než libovolně malé číslo.
Čínský důkaz
Další možností je názorný čínský důkaz, jenž je popsán v knize Devět kapitol matematického
umění. Tato kniha pochází z přibližně stejné doby jako Eukleidovy Základy a v čínské
matematice hraje i podobnou úlohu. Téměř každý čínský matematik do 20. století se na tuto
knihu odkazoval.
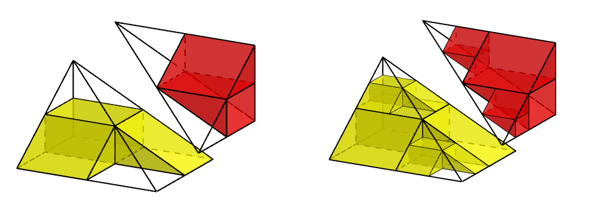
Významný čínský matematik Liu Huie (20–280) popisuje rozklad trojbokého hranolu na
čtyřboký (žlutý) jehlan a trojboký(červený) jehlan – viz obrázek níže. Postupným doplňováním
hranolů ukážeme, že objem žlutého jehlanu je dvakrát větší než objem červeného jehlanu. Odtud
objem jehlanu je třetinou objemu hranolu se shodnou podstavou a výškou. Animace důkazu je
zpracována v materiálu „Volume of Pyramid“ od uživatele Anthony OR.